Considere a tabela

Por qual das funções ou você aproximaria a função ? Justifique sua resposta.
Passo 1
Lembra do teste que eu comentei pra ver se escolhemos a família certa de funções? O teste do alinhamento! Primeiro vamos linearizar ambas as funções:
Isso nos dá a tabela abaixo:
![]()
Repare que usando essa função como aproximação esbarramos com um problema! Nossa linearização não está definida em . Como se não bastasse isso, se jogarmos os pontos em um diagrama de dispersão vamos ficar com isso aqui:
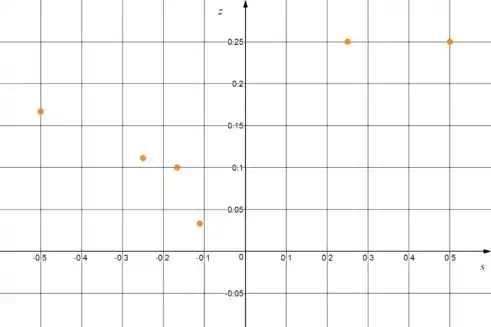
Nada a ver com uma reta essa porcaria né?
Passo 2
A outra aproximação fica:
O que nos dá a tabela abaixo
![]()
E o diagrama de dispersão dessa tabela nos dá:
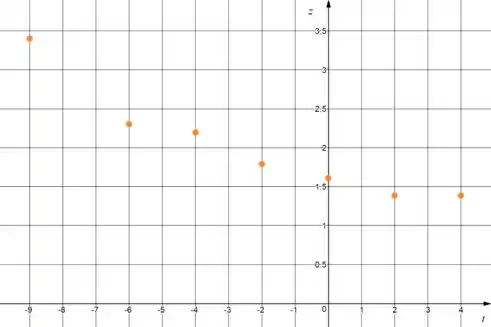
Po, não vou dizer que está uma reta perfeitinha, mas está infinitamente melhor que o outro haha. E aqui a gente não tem o problema da indeterminação em um ponto! Logo, a melhor função para aproximar a é .
Resposta
aproxima melhor a função pelo teste do alinhamento. Além disso, a linearização de possui uma indeterminação em um dos pontos tabelados.