Utilizando o círculo de Mohr, determine as tensões principais e a tensão de cisalhamento máxima no plano e a tensão normal média. Especifique a orientação do elemento em cada caso.
Passo 1
O que está acontecendo?
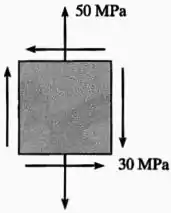
O exercício nos forneceu pela imagem um estado plano de tensões onde:
- Não existe tensão normal na horizontal, de tal forma que:
- Existe na vertical uma tração de , de tal forma que:
- E existe uma tensão de cisalhamento de , mas que está no sentido oposto de sua convenção usual, de tal forma que:
E o que é que ele quer?
Ele quer que a gente use o círculo de Mohr para determinar:
as tensões principais e e suas orientações e ;
& a tensão de cisalhamento máxima no plano , a tensão normal média que acompanha essa tensão de cisalhamento máxima e as orientações que causam essas tensões.
Então, para resolver esse exercício, vamos:
1. Calcular e utilizar esse ponto e o ponto para desenhar o Círculo de Mohr para esse estado de tensões.
2. Usar o teorema de Pitágoras para encontrar o raio do círculo de Mohr e, em seguida, calcular as tensões principais nele.
3. Usar seno, cosseno ou tangente no círculo de Mohr e a função , ou na calculadora para descobrir o valor dos ângulos e .
4. Aplicar e aproveitar o valor já calculado de para definir as tensões pedidas pelo item .
& 5. Aproveitar o ângulo encontrado no terceiro passo para estudar os ângulos no círculo de Mohr e reconhecer os ângulos que levam o elemento à orientação em que a tensão de cisalhamento é máxima.
Passo 2
Então vamos lá!
Como já definimos no passo anterior as tensões , e no nosso estado plano de tensões, já podemos agora calcular :
Desenhar os eixos e :
E em seguida marcar entre esses eixos os pontos:
- ;
- & ,
...para depois ligar esses pontos e usá-los para desenhar nosso círculo:
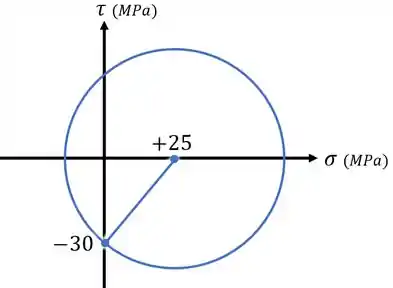
E pronto!
Nosso círculo de Mohr está desenhado.
Agora, devemos usar ele para determinar o que foi pedido pelo exercício.
Passo 3
Primeiro, para descobrirmos as tensões principais usando o círculo de Mohr, precisamos calcular o raio do círculo.
Para tanto, podemos olhar para o desenho do círculo um pouco acima e utilizar o teorema de Pitágoras:
Calculando , encontramos que:
Com isso, podemos calcular as nossas tensões principais e :
Substituindo e , encontramos que:
Passo 4
Agora, vamos observar no nosso círculo de Mohr os ângulos que fazem essas tensões principais aparecerem:
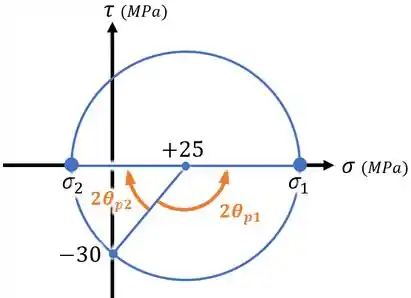
Sendo que aqui, precisamos nos lembrar que:
- Lá no estado de tensões, um ângulo é positivo no sentido anti-horário;
- Então, como desenhamos no nosso círculo de Mohr o eixo apontando para cima, os ângulos no círculo vão ser positivos no sentido horário.
Assim, concluímos que é um ângulo negativo, por estar no sentido anti-horário no círculo de Mohr, enquanto que é um ângulo positivo.
Tendo isso em mente, podemos calcular o valor desses ângulos.
Uma forma de fazer isso é vendo que:
Aí, usando a função da nossa calculadora, e se lembrando de verificar se a calculadora está fornecendo resultados em graus, encontramos que:
O que significa que:
E aí agora, nós sabemos que quando conhecemos um ângulo (nesse caso ), o outro (nesse caso ) pode ser encontrado adicionando ou subtraindo do primeiro.
Dessa forma, temos que:
O que dá:
E assim terminamos o item !
Passo 5
Agora, para resolver o item , nós podemos aproveitar o que calculamos para o item .
Sabemos que a tensão de cisalhamento máxima no plano é sempre igual ao raio do círculo de Mohr, então temos que:
E lá no passo 3, calculamos que , então:
Além disso, sabemos que quando a tensão de cisalhamento no plano é máxima, as tensões normais assumem o valor médio , que já calculamos no passo 2 como:
E assim, em alguns segundos, encontramos as tensões pedidas pelo item .
Passo 6
Mas ainda precisamos encontrar as orientações do elemento que fazem aparecer essas tensões de cisalhamento máximas e normais médias do item .
Para tanto, vamos olhar para os possíveis ângulos no círculo de Mohr que causam essas tensões:
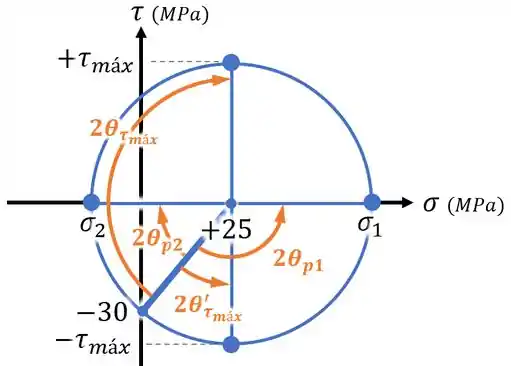
A primeira opção, , está no sentido horário no círculo de Mohr e é portanto positiva (seria negativa caso tivéssemos usado desde o começo um eixo apontando para baixo).
Olhando para o círculo, ainda vemos que ela é maior que o ângulo .
Então, temos que:
Realizando essa soma e dividindo por 2, encontramos que:
Já a segunda opção, :
- é negativa;
- & é “maior” que o ângulo
E no passo passo 4, encontramos que , o que significa que .
Ou seja:
Finalmente, dividindo isso por 2, temos:
Ou seja, o ângulo que podemos usar para rotacionar o nosso elemento e fazer aparecer a tensão de cisalhamento pode ser um ângulo de ou um ângulo de .
E assim finalizamos o nosso exercício!