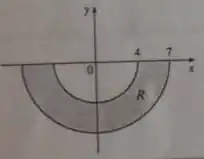
Calcule a área da região representada pelo gráfico em coordenadas polares.
Passo 1
Quando queremos usar uma integral para calcular uma área, temos que montar essa expressão aqui:
Quando queremos montar em coordenadas polares, acontecem duas coisas.
Primeiro, precisamos achar os limites em que variam as coordenadas (o raio) e (o ângulo que o raio forma com o eixo .
Segundo, precisamos usar o jacobiano para escrever aquele . É uma boa ideia ter isso decorado. No caso das coordenadas polares:
Passo 2
Beleza, vamos então calcular os limites de integração de cada variável.
O é mais fácil de visualizar. Lembre sempre que esse é o ângulo em relação ao eixo , medido no sentido anti-horário.
Olhando para a imagem, a nossa região começa só quando já andamos um ângulo (), e termina só quando chegamos no final do ciclo, fazendo um ângulo de (), ou seja:
Passo 3
A gente também pode achar os limites de integração do só olhando a imagem. Para cada valor fixo de , o raio (distância até a origem) de cada ponto da nossa região varia em:
Passo 4
Então pronto, podemos juntar todas essas informações para montar a nossa integral da área:
E agora vamos calcular essa integral. Primeiro integramos em relação a , nesse caso a integral indefinida é :
Resposta
A área da região é .