Seja o conjunto limitado pela curva plana com parametrização dada por :
(veja figura 1). Determine a área de .
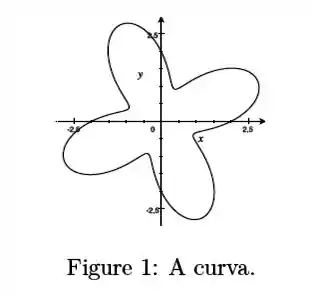
Passo 1
Bom, a área de uma região plana é dada por:
Agora só precisamos escrever essa região na integral.
Passo 2
Vamos usar coordenadaspolares por causa dessess senos e cossenos, ok?
Vamos pensar um pouquinho, as coordenadas polares nos dão que:
Portanto, a parametrização de uma curva em coordenadas polares seria dada por:
Onde é constante ou função de , isso porque, como sabemos, uma curva deve ter um parâmetro! Então, na verdade é isso aqui:
Comparando com a curva do problema
Nós tiramos que
Onde . Percebeu?
Então, se a curva é dada, em coordenadas polares, por essa equação; Como podemos dizer que, para a área , varia desde a origem até a curva, temos:
Com
O que nós acabamos de fazer foi descrever em coordenadas polares.
Passo 3
Agora vamos fazer a mudança polar na integral:
Não se esqueça desse do Jacobiano!
Passo 4
Agora vamos integrar isso ái
Agora precisamos usar essa relação:
Aplicando ao nosso problema, temos: