Se
,
Então é igual a
Passo 1
Nosso exercício pede para que nós calculemos o limite de uma função que ainda não sabemos quem é. Mas podemos descobrir resolvendo a EDO dada. Então vamos descobrir quem é a função e depois calcular o limite.
Pelo que conhecemos de EDO, seria excelente se esta fosse separável, não é mesmo?!
Vamos tentar escrevê-la neste formato charmoso:
Sendo:
Podemos colocar o e evidência, fincando com:
Observa que só o que fizemos foi colocar o em evidência, assim encontramos a multiplicação que precisamos pra nossa EDO separável.
Fazendo:
Pronto! Ela é separável!!
Passo 2
Pra resolvê-la, vamos passar pra o lado esquerdo tudo o que está em função de e para o lado direito tudo o que está em função de
Assim, temos uma função só em de um lado e outra só em do outro lado.
Passo 3
Agora, integramos os dois lados.
Observa que tirei o – de dentro da integral do lado direito! Isso não tem problema nenhum.
Resolvendo primeiro essa integral, temos
Isso é simplesmente um polinômio, e a integral do polinômio nos é dada por
No nosso caso , logo
Para a integral do lado esquerdo vou precisar que você se lembre da integral de
Então pra nossa integral teremos
Passo 4
Com as contas todas feitas podemos voltar a igualdade que tínhamos
Podemos juntar essas duas constantes e chamamos apenas de .
Passo 5
Próximo passo será isolar o Com o que estamos trabalhando agora confesso que parece que vai ser chato. Mas vamos lembrar que, pra tirar algo de dentro do ln, simplesmente aplicamos o exponencial dos dois lados da igualdade.
Podemos cortar o como o E vai ficar assim:
Aqui vou precisar que você lembra de uma outra propriedade do exponencial.
No nosso caso, vamos fazer isso do lado direito. Logo
Exponencial elevado a é simplesmente uma constante que podemos chamar de qualquer coisa, que vou nesse caso chamar de
Além disso vamos deixar o sozinho jogando o 1 para o outro lado subtraindo:
E essa é a função que estávamos procurando.
Passo 6
Vamos calcular o que enunciado pede, que é o limite quando dessa função, vamos fazer:
Observa que podemos separar isso em dois limites, já que é uma soma
O resultado do segundo limite fica 1 mesmo, já o primeira fica
Mas quando vale o exponencial de menos infinito?? Bom, pra gente saber isso, é legal termos o gráfico do exponencial na cabeça.
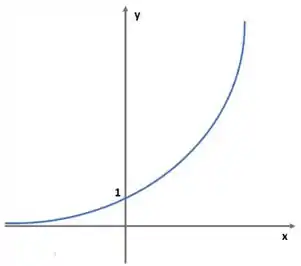
Observa que a função exponencial (curva azul) se aproxima cada vez mais e mais de quanto menor o valor de x, ou seja, quando x está lá no menos infinito, consideramos que a função vai valer zero, tranquilo?
Uma vez que: Podemos então voltar pra o limite
Prontinho