Resolva os problemas de valor inicial abaixo, isto é, encontre a função que satisfaz a equação diferencial e as condições iniciais dadas.
Passo 1
Bom, vamos lá matar mais um questão! Pra começar, vamos reorganizar essa EDO daí pra a forma como estamos mais familiarizados, e conseguir perceber que se trata de uma EDO separável.
Vamos colocar o do outro lado da equação:
A partir daqui vou simplesmente colocar o em evidência
Lindo demais, né? Agora é só eu trocar o por
Agora vou deixar do lado esquerdo da função tudo o que está em função de , e do lado direito tudo o que está em função de tranquilo?
Passo 2
Maravilha! Agora integrando ambos os lados, ficamos com
Vamos calcular cada uma das integrais separadamente e depois igualar o resultado.
A integral da direita é
Pra resolver essa integral precisamos lembrar da propriedade
Por isso temos o resultado encontrado acima, tranquilo?
Passo 3
A integral da esquerda é uma integral já tabelada que vale:
Passo 4
Então substituindo os resultados que encontramos, temos
Podemos juntar as duas constantes e chamar simplesmente de
Vamos então, isolar o
Maravilha, achamos nosso resultado.
Passo 5
Agora usando a condição inicial para descobrirmos o valor dessa constante , ficamos com
Para termos a tangente igual a 1, precisamos que seja igual a , que corresponde ao ângulo de . Veja na tabela:
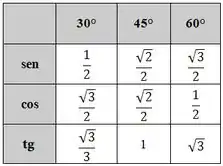
Então:
Portanto a solução é dada por