Para a viga e carregamento mostrados, trace os diagramas de força cortante e momento fletor e determine as equações das curvas de força cortante e momento fletor.
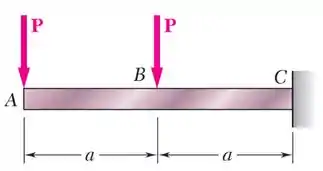
Passo 1
O exercício quer que a gente:
- Determine as equações que descrevem a força cortante e o momento fletor para a viga mostrada;
- E esboce os diagramas de força cortante e momento fletor a partir dessas equações.
Como sempre em um exercício desse tipo, o primeiro passo é fazer o:
![]()
Nesse caso, tendo em mente:
- Que no engaste em , nós vamos ter uma reação na vertical , uma reação na horizontal e um momento ;
- E que, como não há nenhuma outra força horizontal nessa viga, a reação na horizontal vai ser nula/inexistente,
...o nosso DCL (diagrama de corpo livre) fica assim:
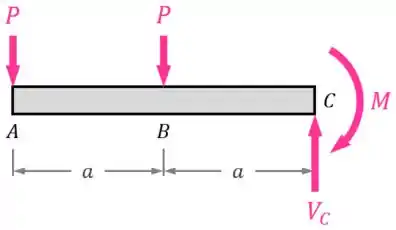
Passo 2
Feito o DCL, podemos seguir para o próximo passo que é o:
![]()
Aqui, temos duas condições de equilíbrio que podemos aplicar:
- O equilíbrio de forças na vertical;
- E o equilíbrio de momentos em relação a um ponto.
Aplicando o equilíbrio de forças na vertical, temos:
E realizando esse somatório, encontramos que:
Em seguida, aplicamos o equilíbrio de momentos em relação ao ponto :
Fazendo esse somatório:
- Sabendo que as forças vão gerar momentos com braços e em relação ao ponto ;
- Sabendo que a força não vai gerar nenhum momento em relação ao ponto ;
- E considerando que os momentos positivos () são aqueles no sentido anti-horário,
...encontramos que:
Passo 3
Agora que já conhecemos todos os esforços (forças e momentos) externos atuantes na nossa viga, podemos seguir para a:
![]()
Existem descontinuidades (nesse caso, forças e momentos concentrados) nos pontos , e dessa viga.
Então devemos analisar as seções entre e e as seções entre e dessa viga.
Usando um eixo começando no ponto e sabendo que não haverá nenhum esforço interno normal nessa viga (uma vez que não há nenhuma força na horizontal), essa análise fica assim:
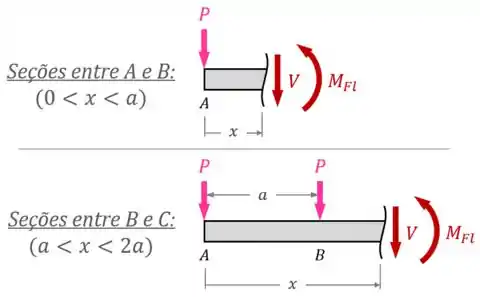
Agora, para terminar a análise, precisamos aplicar as condições de equilíbrio em cada situação.
Para as seções entre e , temos o equilíbrio de forças na vertical:
Que nos diz que:
E também temos o equilíbrio de momentos em relação ao ponto da seção:
Que nos diz que:
Já para as seções entre e , o equilíbrio de forças na vertical fica assim:
Enquanto que o equilíbrio de momentos em relação ao ponto da seção fica assim:
Com o que fizemos até aqui, já conseguimos responder a letra da questão, mas ainda falta os diagramas da força cortante e do momento fletor para respondermos a letra !
Passo 4
Por fim, chegamos ao último passo, que são os:
![]()
Para a força cortante , temos que ela vale quando e que ela vale quando .
Dessa forma, o diagrama da força cortante fica assim:
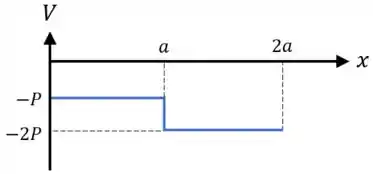
Quanto ao momento fletor , ele é descrito por duas equações de primeiro grau de :
De acordo com a primeira equação, e , enquanto que de acordo com a segunda equação, também é igual à e .
Como as equações que descrevem o momento fletor são de primeiro grau, as linhas que conectam esses pontos (, e ) no diagrama de momento fletor são retas.
Dessa forma, o diagrama do momento fletor fica assim:
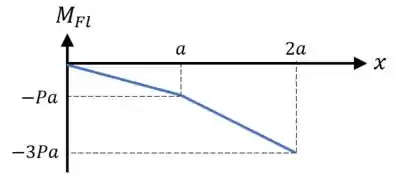
E pronto!
Com esses diagramas dos esforços internos, respondemos ao item e finalizamos o exercício.