Atrito Estático e Cinético
Produzido por Ludovic BeghinTeoria
Fala aí! Chegou a hora de aprendermos a resolver exercícios que envolvem atrito estático e atrito cinético!
Se tiver precisando de uma revisada nesses caras antes de partirmos pro exercícios, não deixa de conferir as páginas aqui do Responde Aí dedicadas a cada um nos links que vou deixar aqui embaixo 👇
⭐ Veja também ⭐
O que é Atrito Estático e Atrito Cinético?
Vamos passar por três conceitos que precisamos ter na ponta do cérebro para tudo ficar bem claro…
Força de Atrito Estático
A força de atrito estático atua em um corpo que está em repouso, quando as demais forças sobre ele não são suficientes para movê-lo.
A fórmula usada para o cálculo da força de atrito estático é:
👉
👉
Força de Atrito Cinético
A força de atrito cinético atua em um corpo que está em movimento.
Quando as forças aplicadas sobre o corpo superam a força de atrito, deixa-se de considerar o atrito estático a favor do atrito cinético, o qual é dado por essa fórmula aqui:
👉
Coeficiente de Atrito
O coeficiente de atrito é uma propriedade definida para um par de materiais e expressa a resistência de se deslizar um sobre o outro.
Esse carinha não é uma propriedade de cada material, viu? É preciso de duas superfícies para defini-lo (você não vai esfregar um objeto no vácuo, né?).
É importante saber que, em situações idênticas, o coeficiente de atrito estático vai sempre ser menor que o coeficiente de atrito cinético.
Isso quer dizer que a força necessária para mover um corpo a partir do repouso é maior do que aquela necessária para mantê-lo em movimento!
Como resolver problemas que envolvem atrito estático e cinético?
Bom, quando te mostrei as equações para os diferentes tipos de atrito, imagino que você tenha reparado que a diferença tá só ali no tal do coeficiente, né?
Então, para resolver um problema que envolve ambos os tipos, ou que não deixa claro logo de cara de qual atrito estamos falando, o segredo é justamente descobrir qual força de atrito atua na situação para podermos usar a fórmula certa.
Vamos resolver juntos o exemplo abaixo, pra eu te mostrar como fazer isso aí. Se preferir, assiste esse videozinho aqui, nele te explico tudo com bastante detalhes, ou segue comigo logo na sequência! 👇
Um bloco de massa m = 5 kg está apoiado em um plano inclinado de ângulo
Quando o enunciado nos pede para “determinar o movimento”, ele quer saber se esse bloco fica parado sobre o plano inclinado ou se ele vai descer. E, caso ele desça, se vai ser de forma acelerada ou retardada.
Beleza, como a gente começa problemas desse tipo? Testando nossas habilidades artísticas! Se liga no desenho:
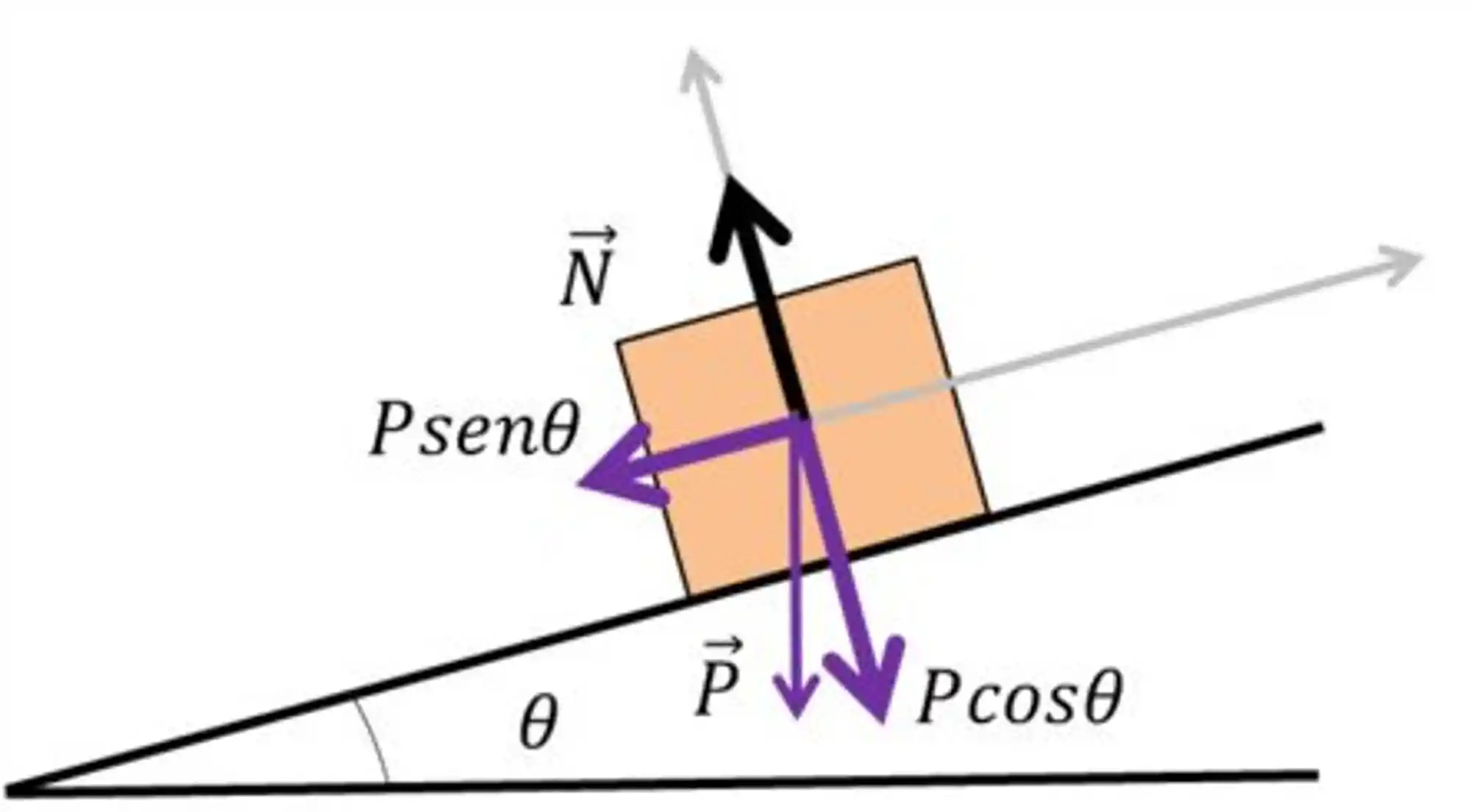
Antes de adicionarmos a força de atrito nesse diagrama, vamos pensar um pouquinho.
A tendência de deslocamento desse bloco é descer pela rampa, certo? Então, a força de atrito aponta no sentido oposto!
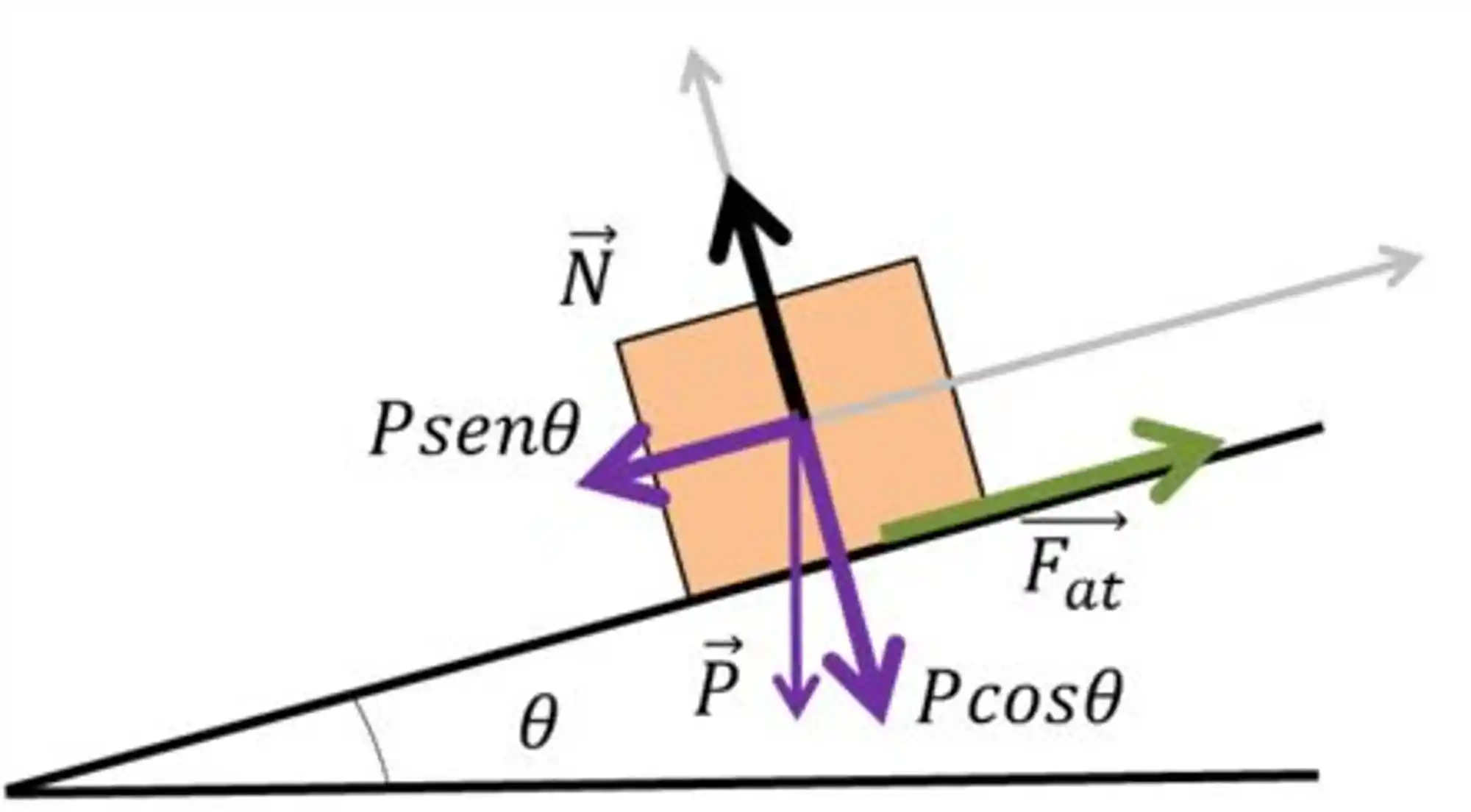
Agora, para esse bloco permanecer parado, a força resultante no sentido do plano inclinado deve ser zero.
Se o corpo está na iminência de movimento, a força de atrito é estática e está no seu valor máximo!
Essa é a força em verde ali na imagem anterior, apontando no sentido de subida da rampa. A única força oposta a ela é aquela
Quer dizer que o bloquinho vai descer o plano!
Isso significa que o atrito que vai atuar aí, na verdade, é o cinético
Agora é a hora de lembrar da famosa segunda lei de Newton:
A força resultante é tudo o que está a favor do movimento, menos aquilo que está contra. No nosso caso:
Portanto, o movimento que o bloco executa é acelerado, com aceleração igual a 3,54 m/s² no sentido de descida do plano inclinado!
Tranquilinho, né? Bora praticar com mais alguns exercícios!
Exercícios Resolvidos
Exercício Resolvido #1
UFF-P1-2014.1-2Q
Dois blocos e , um sobre o outro, deslocam-se rampa abaixo com uma força aplicada sobre o bloco . Os blocos movem-se conjuntamente a velocidade constante de . O coeficiente de atrito cinético entre o bloco e a rampa é , e o coeficiente de atrito estático entre os blocos é . A rampa faz com a superfície horizontal. O bloco da figura pesa e o bloco pesa .
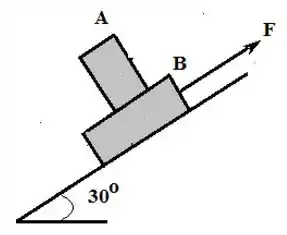
Desenhe dois diagramas do corpo livre separados mostrando as forças que atuam sobre e sobre .
Determine a força necessária para que os blocos apresentem o movimento descrito.
Quais são as intensidades e o sentido da força de atrito no bloco ?
Passo 1
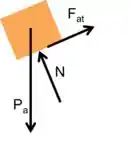
Para o D.C.L dos blocos, temos:
Bloco :
Bloco:
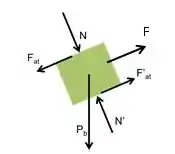
Passo 2
Para determinar a força , vamos montar as equações de movimento para os dois blocos, como os blocos se movem com velocidade constante, a força resultante em ambos é nula. Para o bloco , analisando somente o movimento em , ou seja, ao longo da rampa, temos:
Para o bloco :
Substituindo o valor da , que é cinética, temos:
Substituindo, temos:
Passo 3
No bloco , temos que a força de atrito é dada por:
Resposta
Ver figuras.
Exercício Resolvido #2
PUCRIO-P1-2015.1 Q3
Um corpo de massa escorrega sobre um plano horizontal com coeficiente de atrito cinético e estático , como na figura. Um conjunto de polia e corda sem massa e sem atrito liga este corpo a outro corpo de massa , pendurado na vertical.
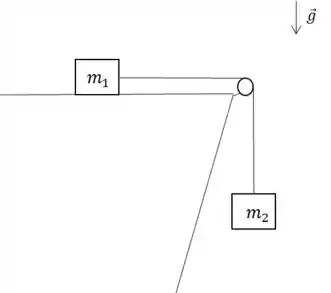
a) Calcule a aceleração do sistema.
b) Calcule a nova aceleração do sistema se colocamos um corpo de massa firmemente preso sobre o corpo 1.
c) Para a situação do item , qual deveria ser a massa mínima de modo que e se movessem em qualquer situação?
Passo 1
Vamos desenhar as forças que estão agindo sobre os corpos no sistema:
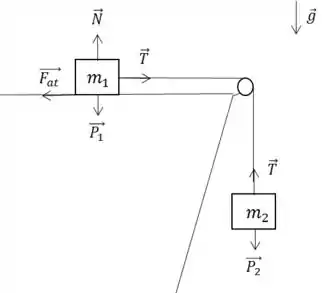
Aplicando a segunda lei de Newton para o bloco . Sabemos que no eixo não tem aceleração, então:
Aplicando no eixo :
Aplicando a segunda lei de Newton para o bloco :
Agora temos duas equações para fazer um sistema:
Somando as duas equações:
Substituindo os dados temos que:
Agora precisamos saber se a força de atrito é estática ou cinética. Vamos calcular a força de atrito estática máxima.
Como a , ou seja, é menor que a força que impulsiona o bloco. Então o bloco está em movimento, e a força de atrito é na verdade a força de atrito cinética. Logo, voltando a nossa equação:
Passo 2
b)
Nesse caso vamos ter exatamente o mesmo sistema, chegando à equação:
Calculando a força de atrito estática máxima:
Como , ou seja, é maior que a força que impulsiona os blocos e . Então o sistema vai ficar no regime estático, prevalecendo a força de atrito estática. Dessa forma, a aceleração do sistema é nula.
Passo 3
c)
Para que o sistema entre no regime cinético, temos que:
No item anterior calculamos essa força de atrito:
Resposta
a)
b)
c)
Exercício Resolvido #3
PUCRIO-P1-B-2013.1 Q3 b c
Seja a situação apresentada na figura abaixo, consistindo de dois blocos de massas (bloco menor) e (bloco maior). Uma força horizontal de módulo é aplicada ao bloco menor. O coeficiente de atrito estático entre os blocos é 0,40 e o de atrito cinético é 0,35. O coeficiente de atrito estático entre o bloco e o solo é 0,30 e o coeficiente de atrito cinético é 0,25.
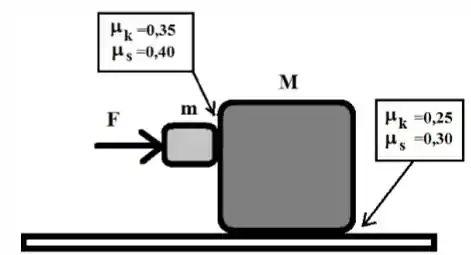
a) Nesta situação, o conjunto dos dois blocos se movimenta na horizontal? Justifique sua resposta através de cálculos explícitos.
b) Calcule a força de atrito entre os dois blocos, argumentando, com cálculos, se esta força é estática ou cinética.
Passo 1
(a)
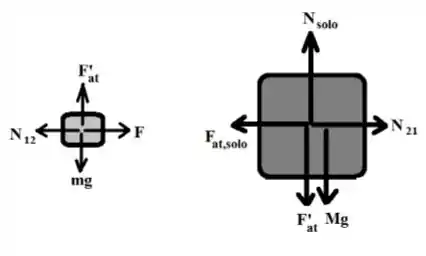
Supondo que o sistema não se movimenta na horizontal, a força que se compensa ao atrito do solo é a própria força aplicada (analisando o conjunto como um todo). Nesta hipótese, temos pra a 2a Lei de Newton: Na vertical:
Na horizontal:
é a força de atrito entre os dois blocos e vai depender se o bloco menor esta escorregando ou não. Como estamos supondo que o sistema esta inicialmente parado na horizontal, podemos observar que e então a força máxima de atrito estática entre os blocos será
Como o peso do bloco menor é:
E este valor é menor que o valor máximo do atrito estático entre os blocos, então o bloco menor fica parado e . Assim:
Assim:
Como então o sistema se movimenta na horizontal.
Passo 2
(b)
Como os dois blocos estão em movimento, então (conclusão do item ). Temos que calcular o valor de (para depois comparar o peso do bloco menor com o valor da força máxima de atrito estático entre os blocos) A 2ª lei de Newton fica neste caso (veja diagrama de forças):
Bloco menor:
Bloco maior:
Horizontal:
Vertical:
Fazendo temos:
Como os blocos estão em movimento.
Daí de , e , temos em função de .
Temos duas opções para : ou ela é igual a (bloco menor não cai) ou ela é cinética e menor que (bloco cai). Supondo que não caia:
e de obtemos:
Com este valor de tem-se:
Força Máxima de atrito estático entre blocos
Como o peso do bloco menor é que é MENOR que a força de atrito estática máxima entre os blocos, então a suposição de que é estática é correta. Assim, o bloco menor está parado em relação à parede do bloco maior. [Se supusermos que inicialmente o bloco menor está se movendo, calculamos através de cinética e chegaremos a uma inconsistência.]
CONCLUSÃO: a força de atrito entre os blocos é ESTÁTICA e seu valor é o peso do bloco menor, .
Resposta
(a) O sistema se movimenta na horizontal.
(b) A força de atrito entre os blocos é estática e seu valor é
Exercício Resolvido #4
UFRJ-Física 1-P1 2012.1 Q1
Um bloco de massa está sob a ação de uma força horizontal constante sobre uma superficie horizontal sem atrito. Sobre ele há um bloco de massa , preso à esquerda por um fio ideal. Este fio passa por uma roldana ideal que encontra-se fixa a uma parede vertical, e o conecta ao bloco de massa . Os segmentos do fio são paralelos ao plano horizontal; vide a figura abaixo. Suponha que haja atrito entre os blocos em contato entre si. Considere como conhecidos os valores dos coeficientes de atrito estático e cinético , as massas e e o módulo da aceleração da gravidade .
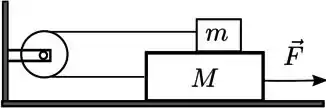
- Isole os blocos e represente por meio de um diagrama de corpo livre todas as forças que atuam em cada um deles.
- Suponha inicialmente que os blocos estejam em repouso. Determine o valor máximo do módulo de , para que o sistema permaneça em repouso.
- Considere agora que , cujo módulo é igual a , seja capaz de colocar os blocos em movimento com aceleração constante. Para o intervalo de tempo no qual os blocos permanecem em contanto entre si, determine os vetores aceleração de cada bloco em função de , , , e .
- Determine o módulo da tração do fio, para o caso do item anterior c)
Passo 1
Primeiramente vamos escrever os dados no enunciado
Vamos fazer isso para verificar depois cada resposta para ver se está de acordo com os dados do problema.
Passo 2
a)
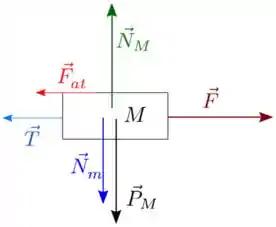
Vamos responder as perguntas do passo a passo para colocar as forças, primeiro do bloco de massa .
- A massa dele é considerada?
- Ela esta encostada em alguma superfície?
- Tem algum fio?
- Tem mola?
- Tem atrito?
Sim, ele tem massa.
Sim, o bloco está apoiado no chão e no bloco de massa .
Sim, existe um fio.
Não, não existe mola atuando.
Sim, existe atrito entre os blocos
O DCL fica
Passo 3
Vamos responder as perguntas do passo a passo para colocar as forças, primeiro do bloco de massa .
- A massa dele é considerada?
- Ela esta encostada em alguma superfície?
- Tem algum fio?
- Tem mola?
- Tem atrito?
Sim, ele tem massa.
Sim, o bloco está apoiado no bloco de massa .
Sim, existe um fio.
Não, não existe mola atuando.
Sim, existe atrito entre os blocos
O DCL fica
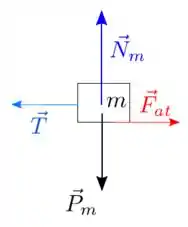
Repara que quando o bloco de baixo é puxado, para que o bloco de cima fique parado a força de atrito deve ser para a direita, porque ao puxar o bloco de baixo ele puxa o fio, que por sua vez puxa o bloco de cima para a esquerda.
A força de atrito no bloco de baixo será oposta porque o bloco de cima tende a segurar o movimento.
Passo 4
b)
O valor máximo da força vai ser quando a força de atrito estática entre os blocos for máxima. O que isso significa? Que podemos fazer
Vamos fazer o equilíbrio em cada bloco.
Começando no bloco de massa
Vamos começar pelo .
Passo 5
Fazendo equilíbrio no agora
Passo 6
Vamos para o equil��brio no bloco de massa
No
Passo 7
Enquanto isso no
Então
Passo 8
c)
Vamos reescrever os dados
O DCL nesse caso fica igual a diferença é que os blocos vão se mover. O diferente dessa questão é que o bloco de massa vai se mover para a esquerda enquanto o bloco de massa vai se mover para a direita.
Isso faz com que
Passo 9
As equações ao longo do não vai mudar, relembrando
Vamos agora para o equilíbrio ao longo do do bloco de massa , tomando como sentido positivo de forças atuanto para direita.
Temos o caso da força de atrito dinâmica
Passo 10
Isso não resolve o problema, vamos agora para o equilíbrio da bloco ao longo do
Passo 11
Temos
Vamos multiplicar a primeira equação por
Somando as duas equações
Passo 12
Beleza achamos o módulo da aceleração, lembra que
E ambas estão na horizontal?
Passo 13
d)
Das equações temos
Igualando os denominadores
Essa ultima foi meio tensa as contas hein!!
Resposta
Exercício Resolvido #5
P1- PUCRJ-Fisica I-2011.2- Q3
A figura a seguir mostra o bloco () conectado a uma parede rígida por uma corda ideal, repousando sobre o bloco (). O bloco está submetido a uma força horizontal para a direita que pode variar em módulo. Adote .
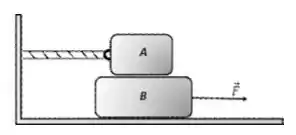
O sistema repousa sobre um solo que oferece atrito desprezível. Só existe atrito na superfície entre os blocos (). A situação inicial é de repouso.
a) Faça o diagrama de corpo livre para cada um dos blocos isoladamente. Não calcule valores, apenas nomeie todas as forças que agem em cada bloco.
b) Para o caso em que , e supondo que a corda não se rompe, calcule os vetores força de todas as outras forças que agem sobre os blocos. Use o sistema de coordenadas padrão: eixo positivo apontando para a direita, eixo positivo apontando para cima. (Dica: calcule primeiro o valor da fora de atrito estático máximo entre os blocos.)
c) Para o caso em que , calcule os módulos da aceleração do bloco e da força de tração da corda sobre o bloco , supondo que a corda não se rompe.
d) Suponha agora que a corda não exista, mas que todos os outros dados do enunciado principal sejam repetidos. Calcule o valor máximo que a força pode assumir de tal modo que não haja deslizamento relativo entre os blocos, ou seja, eles aceleram juntos.
Passo 1
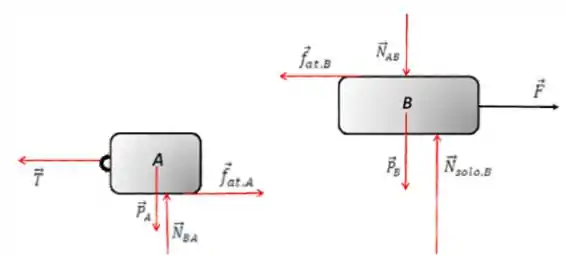
a)
Essa parte é simples, basta não se esquecer das forças de ação e reação de contato (normal e atrito).
Passo 2
b)
Vamos seguir a dica do enunciado e calcular primeiramente o valor da força de atrito máxima entre os blocos. Para isso, temos que primeiro encontrar o valor da força normal.
Aplicando a segunda lei de Newton para as forças sobre o bloco , no eixo , sabendo que :
Agora sim, vamos calcular o valor máximo da força de atrito estática entre os blocos:
Como a força é menor que a força de atrito estática máxima, o sistema se manterá em repouso. Sendo assim, o módulo da força de atrito será igual ao de .
Calculando as demais forças, temos as forças sobre o bloco no eixo , sabendo que :
E também as forças sobre o bloco no eixo , sabendo que :
Finalmente, as forças sobre o bloco no eixo , sabendo que :
Passo 3
c)
Agora, como o módulo de supera o atrito estático máximo, o bloco sairá do repouso (o bloco não, pois a corda não se rompe). Como há deslizamento entre as superfícies dos blocos, o atrito passa a ser cinético e de valor:
Assim, para o bloco , teremos, no eixo , sabendo que :
Para o bloco , teremos, no eixo :
Passo 4
d)
Na situação limite de não deslizamento relativo entre os blocos, o atrito entre eles atingirá o valor estático máximo , e essa força de atrito será a própria resultante horizontal agindo sobre o bloco :
Como o bloco move-se junto com o bloco , podemos considerar o sistema composto pelos dois blocos como um único corpo rígido, de massa total igual a , com a aceleração calculada de . Como a força é a única a atuar na horizontal sobre o sistema composto, ela é a própria resultante horizontal:
Resposta
a)
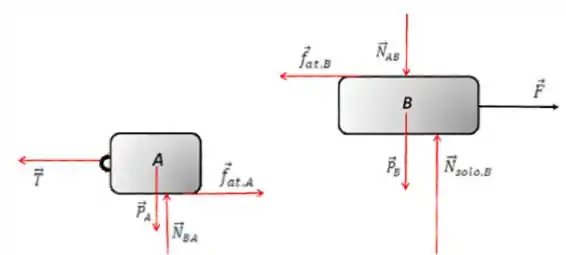
b)
c)
d)
Exercício Resolvido #6
UNICAMP-P1- 2015.1-D1
Na figura abaixo, as massas dos blocos 2 e 3 são e , respectivamente. O coeficiente de atrito cinético entre o bloco 2 e a mesa é 0,10 enquanto o coeficiente de atrito estático é 0,20. Despreze o atrito entre os blocos 1 e 2.
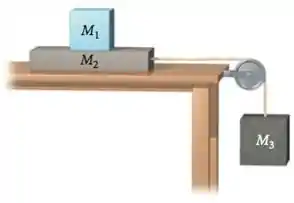
a) Usando a 3a Lei de Newton, faça o diagrama do corpo livre para cada um dos três blocos, indicando todos os pares de ação e reação.
b) Qual deve ser o valor mínimo da massa do bloco 1 para que o bloco 2 não se mova?
c) Calcule a aceleração do sistema se o bloco 1 é levantado.
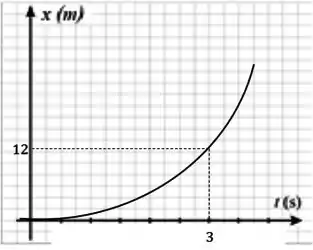
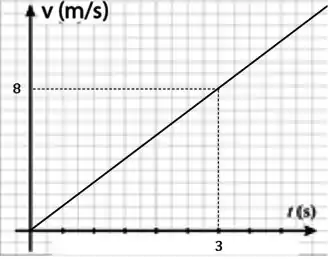
d) Esboce os gráficos da velocidade e da posição do bloco 2, desde o momento em que o bloco 1 é levantado até após este momento.
Passo 1
a)
As únicas forças de ação e reação do sistema são as forças de contato (forças Normais). São as forças e entre os blocos 1 e 2.
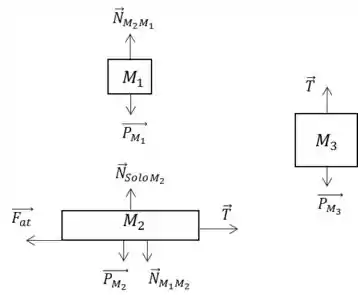
Passo 2
b)
Aplicando a segunda lei de Newton na direção do movimento. Podemos perceber que o bloco 1 não possui forças na horizontal, logo ele não se movimentará. Para os demais blocos ficará:
Bloco 2:
Bloco 3:
Se somarmos a equação do bloco 2 com a equação do bloco 3, teremos:
Ou seja, para o sistema não entrar em movimento, temos que ter:
Como estamos falando de um sistema estático, então essa força de atrito é a força de atrito estática máxima:
Como o bloco 2 está em equilíbrio na vertical, vamos ter:
O bloco 1 também está em equilíbrio na vertical, então vamos ter:
Como , podemos substituir na equação de equilíbrio vertical do bloco 2:
Agora sim! Finalmente chegamos onde queríamos, relacionar tudo isso com o peso do bloco 1. Agora vamos substituir na equação do movimento que fizemos lá atrás:
Substituindo os dados:
Passo 3
c)
Com o bloco 1 levantado vamos chegar a mesma equação do item anterior:
Substituindo a fórmula da força de atrito:
Só que como não temos mais o contato do bloco 1 com o bloco 2. Por conta, aplicando o equilíbrio na vertical para o bloco 2:
Substituindo:
Substituindo os dados:
Passo 4
d)
Se adotarmos a posição do bloco 2 como a origem, podemos calcular a velocidade e posição após .
Como a posição depende do tempo ao quadrado, essa função será representada como uma parábola.
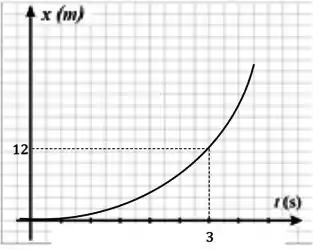
Agora calculando a velocidade em :
Como a velocidade depende linearmente do tempo, então essa função será representada por uma reta.
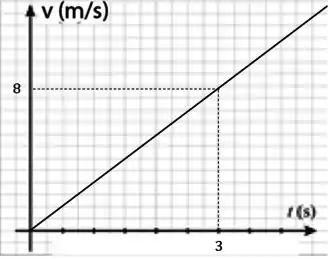
Resposta
a)
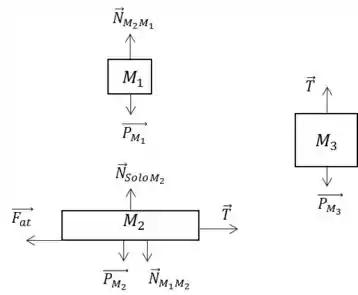
b)
c)
d)