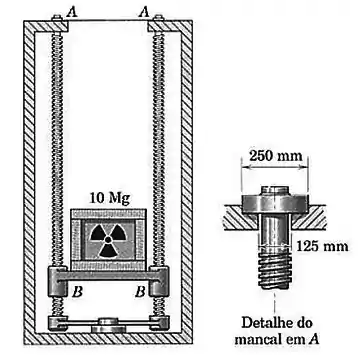
O caixote de é abaixado para uma câmara de armazenamento subterrânea em um elevador de dois parafusos projetado como mostrado. Cada parafuso tem uma massa de , um diâmetro médio de e uma rosca quadrada simples com um passo de . Os parafusos são girados em sincronismo por uma unidade motorizada na base do dispositivo. Toda a massa do caixote, dos parafusos e da plataforma de do elevador é sustentada uniformemente por mancais radiais planos em , cada um tendo um diâmetro externo de e um diâmetro interno de . A pressão nos mancais é considerada uniforme sobre toda a superfície dos mancais. Se o coeficiente de atrito para os mancais radiais e os parafusos em vale , calcule o torque que deve ser aplicado a cada parafuso para suspender o elevador e para abaixar o elevador.

Sabendo que o coeficiente de atrito () vale , vamos ter que o ângulo de atrito () será:

A carga axial vai o peso do caixote somado com o peso da plataforma:

Repare que a unidade de massa foi dada em () e é preciso passar para () para calcular o peso!

Então, o momento necessário para apertar cada parafuso será:

Repare que a carga axial foi dividida pela metade já que cada parafuso suporta metade do peso total!

E para abaixar o elevador precisamos afrouxar o parafuso, então vamos ter que:

Agora vamos calcular o momento devido ao atrito nos mancais...

Repare que foi dito no enunciado que a pressão nos mancais é uniforme. Mas pela figura que mostra o mancal, vemos que ele tem o formato de um anel, ou seja, possui um raio interno () e um raio externo .

Nesse caso, temos que usar a seguinte equação:

A força vai ser o peso total do sistema:

Então, para cada mancal vamos ter que:

Então, para suspender o elevador o momento total será:

E para abaixar o elevador vamos ter que o momento total vai ser de: