Determine a expressão para o torque necessário para girar o eixo cuja pressão axial é sustentada por um mancal cônico. O coeficiente de atrito é e a pressão no mancal é constante.
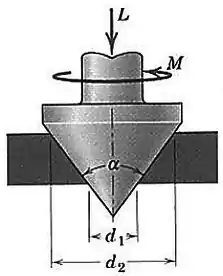
Passo 1
Opa! Esse mancal aí é diferente, né?
Mas vamos dar um jeito resolver esse problema, fique tranquilo!
A pressão nesse caso também não é constante, já que a seção transversal é variável. No caso constante, nós usamos:
Nesse caso, vamos usar:
Passo 2
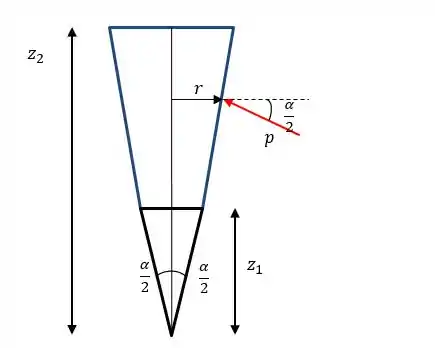
A área que queremos integrar é definida pelos limites e
Mas quem é
Geralmente escrevemos algo como:
Mas no nosso caso, a nossa dimensão está curvada, já que a superfície é inclinada. Veja no triângulo abaixo:
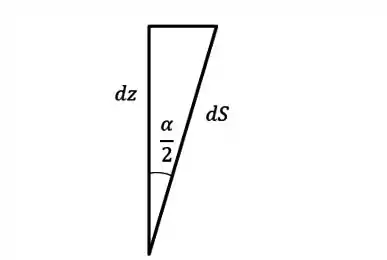
Desse modo, podemos escrever:
Assim:
Vamos agora escrever em função de . Observe o nosso triângulo:
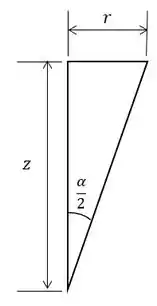
Perceba que:
Então, substituindo na nossa equação de temos que:
Passo 3
Perceba também que a pressão faz um ângulo com a horizontal. Nós estamos integrando para achar , que é totalmente vertical. Por isso que estamos integrando que é a componente vertical de e é dada por:
Ufa! Jogando tudo na integral:
Arrumando isso aí, temos que:
Passo 4
Vamos integrar em Mas quais são os limites de integração?
Usando dois triângulos marotos, vamos usar a trigonometria para achar esses limites, que são coordenadas de
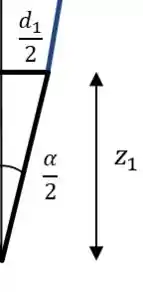
Assim:
E:
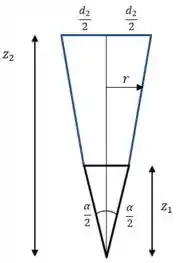
Assim:
Agora já podemos integrar:
Mas já achamos os valores de e , então vamos substituí-los:
Simplificando isso aí, vamos ter que:
Como o que precisamos saber é a pressão , vamos isolá-la:
Pronto! Vamos agora falar do momento.
Passo 5
O momento é dado por:
A boa notícia é que já definimos e. Então, basta a gente tacar tudo ali naquela integral:
Arrumando essa bagunça:
Agora é só substituir os limites:
Vamos cortar as tangentes ao cubo com a tangente ao quadrado:
Lembrando que , podemos escrever a nossa equação assim:
Então, cortando os cossenos, vai nos restar:
Ufa! Agora é só substituir o valor que encontramos para pressão em função de nesta equação do momento aí de cima:
Assim: