O peso do tambor e de seu cabo é de e o coeficiente de atrito para o mancal vale . Determine a força necessária para suspender o cilindro de se o atrito no mancal é desprezível e incluído na análise. O peso do eixo é desprezível.
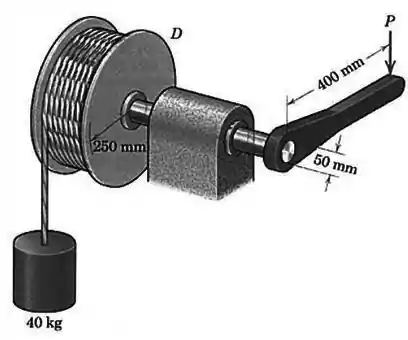
Passo 1
Para o primeiro caso em que o atrito é zero, vamos ter que:
Então, podemos desenhar nosso sistema assim:
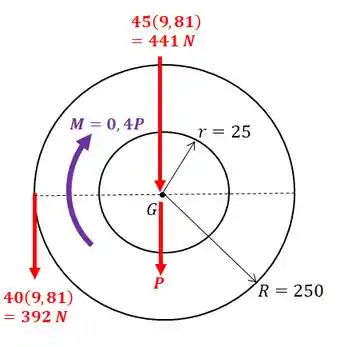
Repare que levamos a força para o ponto central do tambor, mas para fazer isso temos que levar o momento que esta força faz com relação a este ponto:
Beleza?
Passo 2
Para achar o valor da força é só fazermos o somatório de momentos com relação ao ponto :
Passo 3
Agora vamos considerar o atrito, então:
Então, precisamos calcular o ângulo :
Portanto, será:
Passo 4
Para esta nova situação, podemos desenhar o nosso sistema assim:
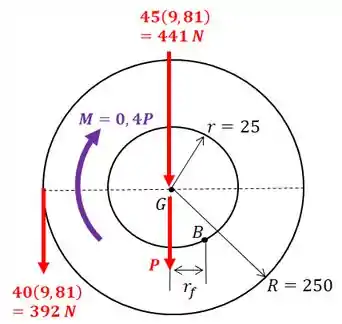
Para achar o valor da força vamos fazer o somatório de momentos com relação ao ponto :