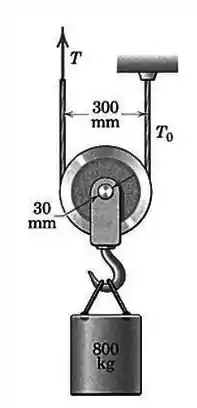
Determine a força trativa no cabo para suspender a carga de se o coeficiente de atrito para o mancal de vale . Determine, também, a força trativa na seção estacionária do cabo. As massas do cabo e da polia são pequenas e podem ser desprezadas.
Passo 1
Podemos desenhar nosso sistema assim:
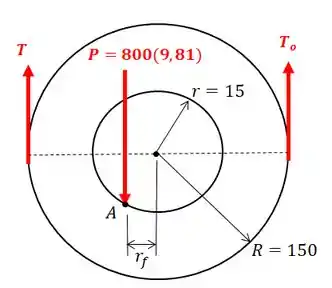
O é calculado assim:
Mas antes temos que calcular o ângulo :
Então, será igual a:
Passo 2
Para determinar as forças, temos que usar as equações de equilíbrio.
Vamos começar fazendo o somatório de momentos com relação ao ponto , considerando o momento positivo girando no sentido anti-horário:
Passo 3
Agora vamos fazer o equilíbrio das forças verticais:
Vamos substituir nesta equação que acabamos de achar:
E vai ser:
Resposta
Exercícios de Livros Relacionados
O disco de embreagem é usado nas transmissões de automóveis padrão. Se quatro molas são usadas para manter os dois discos A e B juntas, determine a força em cada mola necessária para transmitir um mom
Se a mola exerce uma força de 4500N sobre o bloco determine o torque M necessário para girar o eixo. O coeficiente de atrito estático em todas as superfícies de contato é μ s = 0,3 .
135- Calcule o momento M aplicado ao cilindro inferior do par, ambos com 20k g , que permitirá que eles rolem para baixo lentamente. Os coeficientes de atrito estático e dinâmico para todas as superfí
A roldana dupla mostrada na figura é fixada a um eixo de 10m m de raio que se ajusta com folga a um mancal fixo. Sabendo que o coeficiente de atrito estático entre o eixo e o mancal pouco lubrificado
Uma alavanca de peso desprezível está encaixada com folga em um eixo de 75m m de diâmetro. Observa-se que a alavanca apenas inicia um movimento de rotação se a massa de 3k g é adicionada em C . Determ