O Método da Bisseção do Cálculo Numérico é um método que nos ajudará a:
- Encontrar zeros de funções reais
- Resolver Sistemas Lineares
- Integrar Funções
- Derivar Funções
- Interpolar Funções
- Resolver EDO’s
Passo 1
Fa Aíí! Bom, vamos relembrar um pouco sobre o método da Bisseção para entender no que ele nos ajuda?!

O método da Bisseção é um método de intervalos onde conseguimos encontrar estimativas (aproximações) para a raiz da função: Tiramos a média entre os dois pontos do intervalo e vemos onde está a raiz.
Por exemplo, se temos um intervalo
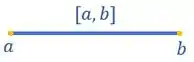
Dividimos esse intervalo em dois intervalos utilizando o ponto médio:
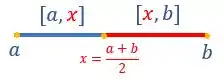
Agora ficamos com dois intervalos de tamanhos iguais, e . Para descobrirmos qual deles tem a raiz é só fazermos e analisar se o valor é maior ou menor que zero.
Ou seja, analisando as opções do intervalo, a nossa resposta é a letra A!