Utilize o método da Bisseção para estimar a raiz da função . Utilize a precisão de
Passo 1
Fala Aííí!! Como podemos atacar esse exercício? Nós precisamos utilizar o método da bisseção, certo?! Belê, mas como vamos fazer isso? Primeiro damos uma aproximação inicial para a raiz dentro de um intervalo, aí nós vamos refinando através de processos iterativos. Vamos ver como vai funcionar na prática?

Passo 2
A primeira coisa que vamos fazer é localizar um intervalo que contenha a raiz da função (que será nosso pontapé inicial). Esse intervalo costuma ser uma estimativa bem grosseira, que vai passar pelo processo de refinamento pra diminuir e ficar bem pequenininho. Beleza?!
Vamos então começar chutando um intervalo que vai de a .
Mas é só chutar o intervalo?!

Não!! Precisamos aplicar o Teorema de Bolzano para verificar se esse intervalo de fato contém uma raiz. Assim, aplicando o teorema de Bolzano no intervalo , temos
E
Assim, fazendo
OPA! A multiplicação deu um valor menor do que zero! O teorema de Bolzano então nos garante que existe pelo menos uma raiz entre o intervalo .
Show de bola?!
Passo 3
Depois que escolhemos as aproximações iniciais para o intervalo na primeira fase, começamos o processo de iterações (onde cada bateria de cálculo conta como uma iteração) para melhorarmos varias vezes até encontrar uma aproximação próxima da raíz real.
Tá... mas como vamos refinar o resultado aqui no método da Bisseção?

Aqui no método da bisseção o algoritmo é o seguinte:
Tiramos a média entre os dois pontos do intervalo e vemos onde está a raiz. Bem simples né?
Por exemplo, se temos um intervalo , fazemos:
Agora ficamos com dois intervalos de tamanhos iguais, e . Para descobrirmos qual deles tem a raiz é só fazermos e analisar se o valor é maior ou menor que zero. Se o resultado desse produto for menor que zero, a raiz está aí ! Se for maior, a raiz ta no intervalo . Então, esse nosso novo (e menor) intervalo vai passar a ser o novo e vamos repetindo o processo! Muita informação??? Vamos fazer juntos esse algoritmo agora!

O nosso intervalo que contém a raiz é o , certo?
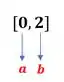
Vamos fazer agora 1ª iteração utilizando
Substituindo os valores,
Beleza?!
Agora vamos partir o nosso intervalo inicial em dois intervalos:
E
Show de bola?!

Agora em qual desses dois intervalos está a minha raiz? Vamos aplicar o teorema de Bolzano para saber!!
Aplicando o teorema de Bolzano no intervalo
Temos que
E
Assim, fazendo
OPA! A multiplicação deu um valor menor do que zero! O teorema de Bolzano então nos garante que existe pelo menos uma raiz entre o intervalo .
Passo 4
Beleza... Conseguimos refinar um pouco o nosso intervalo com esse método iterativo da Bisseção, mas como eu sei que estou próximo o suficiente do valor real? Aí que entram os critérios de parada.

O que vamos fazer aqui é fazer a diferença entre os extremos do intervalo e verificar se ele é menor do que a precisão dada no enunciado . Ou seja,
Substituindo os valores, temos
OPA! Isso não é verdade! Temos que é maior do que ou seja, precisamos fazer mais iterações para chegar na aproximação ideal do exercício!! Então vamos continuar!
Passo 5
Agora utilizaremos o intervalo para fazer a segunda iteração:
Podemos partir então o intervalo em dois:
E
Show de bola?! Precisamos verificar em qual desses dois intervalos está a nossa raiz pelo teorema de Bolzano. Verificando no intervalo :
E
Assim, fazendo
OPA! A multiplicação deu um valor menor do que zero! O teorema de Bolzano então nos garante que existe pelo menos uma raiz entre o intervalo .

Vamos agora aplicar o critério de parada para ver se já atingimos a precisão dada no enunciado:
Substituindo os valores, temos
OPA! Isso é verdade! Temos que é menor do que ou seja, já podemos parar por aqui!! Caso tivéssemos uma igualdade aqui que não fosse verdadeira, precisaríamos fazer mais iterações para chegar na aproximação ideal do exercício!! Show de bola?!
Assim, conseguimos estimar a raiz da nossa função