Um trocador de calor de tubo duplo com parede fina e escoamento paralelo é utilizado para aquecer um produto químico, cujo calor específico é , com água quente .
O produto químico entra a com uma taxa de , enquanto a água entra a com uma taxa de . A superfície de transferência de calor do trocador de calor é de e o coeficiente global de transferência de calor é .
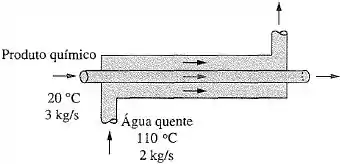
Determinar as temperaturas de saída do produto químico e da água.
Passo 1
As temperaturas de saída podem ser calculadas pelas seguintes equações:
Show de bola! Nós temos as temperaturas de entrada dos fluidos, temos como calcular as taxas de capacidade térmica, mas não temos a taxa de transferência de calor.
Então vamos atrás desse cara usando o Método da Eficiência e NUT. Dessa forma, a taxa de transferência de calor será dada por:
Vamos tratar de cada termo separadamente, beleza?
Passo 2
Vamos começar tratando da taxa de transferência de calor máxima possível , que é dada por:
Para calcular a menor taxa de capacidade térmica, temos que calcular as taxas de capacidade térmica dos dois fluidos.
Como o menor valor corresponde ao do fluido frio (água), teremos:
Dessa forma, a taxa de transferência de calor máxima possível será:
![]()
Passo 3
Para calcular a efetividade da transferência de calor, vamos precisar do NUT e da razão das capacidades, dados por:
Como estamos trabalhando com um trocador de calor de escoamento paralelo, a relação mais adequada para a efetividade será:
Substituindo os valores:
![]()
Passo 4
A taxa de transferência de calor será:
Assim, as temperaturas de saída dos fluidos serão:
![]()
![]()