Seja a função . Considere o método da Posição Falsa para cálculo da raiz, e os valores iniciais para pesquisa e . Assim, empregando o método, na iteração seguinte, a raiz deverá ser pesquisada no valor:
- 0,5
Passo 1
Fala Aííí!! No método da Bisseção nós vimos um algoritmo nada refinado né? Era só ir tirando a média haha, o que fazia com que perdêssemos um tempinho. Aqui a conta é um pouquinho mais complexa. No método da Posição Falsa vamos encontrar nossa estimativa de cada iteração fazendo:
Beleza?! De resto é tudo igual!! Continuamos as iterações até que o critério de parada seja atingido!
Vamos então pras continhas?!

Passo 2
Os valores iniciais dados no enunciado são e ! Logo, o nosso intervalo inicial é
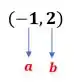
A primeira coisa que vamos fazer é aplicar o Teorema de Bolzano para verificar se o intervalo dado no enunciado de fato contém uma raiz. Assim, aplicando o teorema de Bolzano no intervalo , temos
Assim,
E
Assim, fazendo
OPA! A multiplicação deu um valor menor do que zero! O teorema de Bolzano então nos garante que existe pelo menos uma raiz entre o intervalo .

Passo 3
Agora vamos para o processo de iteração! No método da Falsa posição utilizamos o
Substituindo os valores, temos
Fazendo as continhas, temos que
Show de bola?!
Logo, a nossa resposta é a letra E!