Seja com um zero no intervalo . Calcule a raiz de com precisão de utilizando o método da posição falsa.
Passo 1
Vamos láá!! No método da Posição Falsa vamos encontrar nossa estimativa de cada iteração fazendo:
Beleza?! De resto é tudo igual ao método da Bisseção!! Continuamos as iterações até que o critério de parada seja atingido! No caso aqui a nossa precisão é de !

Passo 2
Os valores iniciais dados no enunciado são e ! Logo, o nosso intervalo inicial é
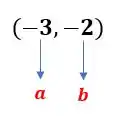
A primeira coisa que vamos fazer é aplicar o Teorema de Bolzano para verificar se o intervalo dado no enunciado de fato contém uma raiz. Assim, aplicando o teorema de Bolzano no intervalo , temos
Assim,
E
Assim, fazendo
OPA! A multiplicação deu um valor menor do que zero! O teorema de Bolzano então nos garante que existe pelo menos uma raiz entre o intervalo .
Passo 3
Agora vamos para o processo de iteração! No método da Falsa posição utilizamos o
Substituindo os valores, temos
Fazendo as continhas, temos que
Agora podemos dividir em dois intervalos:
E
Show de bola?!

Agora em qual desses dois intervalos está a minha raiz? Vamos aplicar o teorema de Bolzano para saber!!
Aplicando o teorema de Bolzano no intervalo , temos
E
Assim,
OPA! A multiplicação deu um valor menor do que zero! O teorema de Bolzano então nos garante que existe pelo menos uma raiz entre o intervalo .
Será que já alcançamos o nosso critério de parada?
Critério de Parada:
Como não alcançamos o critério de parada, continuamos as iterações.
Passo 4
Vamos continuar com o mesmo raciocínio anterior, só que com o novo intervalo
Iteração :
E assim podemos dividir em dois intervalos
E
Agora precisamos utilizar o teorema de Bolzano para encontrar em qual dos dois intervalos está a raiz. Fazendo os testes, verificamos que a raiz está no intervalo , pois
Logo, nosso novo intervalo será formado por e . Temos então que:
Critério de Parada:
Como não alcançamos o critério de parada continuamos as iterações.

Passo 5
Agora estamos com o intervalo
Iteração :
Logo, nosso novo intervalo será formado por e . Temos então que:
Critério de Parada:
Como não alcançamos o critério de parada continuamos as iterações.
Intervalo:
Iteração :
Logo, nosso novo intervalo será formado por e . Temos então que:
Critério de Parada:
Como não alcançamos o critério de parada continuamos as iterações.
Intervalo:
Iteração :
Logo, nosso novo intervalo será formado por e . Temos então que:
Critério de Parada:
Como não alcançamos o critério de parada continuamos as iterações.
Iteração :
Logo, nosso novo intervalo será formado por e . Temos então que:
Critério de Parada:
Pronto, chegamos na aproximação com a precisão pedida. A raiz é então, com precisão de , .
