De acordo com o gráfico apresente, ao menos, três integrais triplas iteradas que representam o volume do sólido em questão.
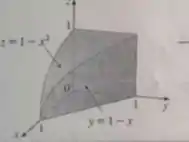
Passo 1
Ok, basicamente o que nós vamos fazer para obter três integrais diferentes, é alternar qual das constantes está limitada por constantes.
Por exemplo, vamos fixar por constantes. Olhando para a imagem, a coordenada de qualquer ponto da figura está no intervalo:
Concorda? E agora você tem que se fazer a seguinte pergunta: para um ponto fixo no , em qual intervalo variam as outras coordenadas?
Bom, vamos olhar para o primeiro. Vamos representar o valor fixo de por uma reta amarela (é só um exemplo, aquela reta poderia estar em qualquer entre e )
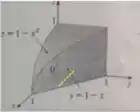
Em qual intervalo varia a coordenada dos pontos daquela reta? Bom, todos começam no zero e vão até aquele reta , que é o mesmo que .
Ou seja:
E o ? Assim como as outras duas, ele começa no zero, mas é limitado por uma função . Ou seja, para cada e fixos, o varia em:
Agora é só jogar isso em uma integral tripla:
Cuidado para não errar a ordem dos diferenciais!
Beleza, se você entendeu essa, as outras vão ser tranquilas também.
Passo 2
Como nós falamos lá em cima, a única coisa que vai mudar é: qual das variáveis é limitada por constantes.
Já fizemos par a o , agora vamos pegar o . Todos os pontos que estão naquele volume têm coordenada dentro de qual intervalo?
Ótimo. Agora vamos àquela pergunta importantíssima: para cada fixo, em qual intervalo variam os valores de ? Vamos um qualquer por uma reta amarela:
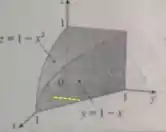
Dá pra visualizar o intervalo? Todos os pontos começam no , e vão até ! Ou seja:
E agora o vai continuar como era no item anterior! Para cada e fixos, o varia em:
Então nossa segunda integral é:
Mudou bem pouco né? Mas é diferente.
Passo 3
Para finalizar, vamos pegar o caso em que é limitado por constantes. Olhando para a imagem, todos os pontos do volume tem coordenada variando dentro de qual intervalo?
Certo? É impossível achar um ponto no volume que tenha coordenada fora desse intervalo.
Agora vamos à pergunta: para cada fixo, em qual intervalo varia o ? (poderia perguntar do também, a ordem não importa). Vamos voltar à nossa reta amarela:
![]()
A coordenada dos pontos daquela reta sempre começam no (para cada fixo), mas até onde eles vão? Bom, eles estão limitados por aquela função , que pode ser reescrita como (não precisa colocar o , já que estamos no primeiro octante).
Então:
E agora vamos ao . Para cada e fixos, onde varia o ? Tranquilo, o só depende do , e vai variar do até aquela função , ou seja:
E a nossa terceira integral é:
Pronto! Escrevemos três integrais diferentes que calculam o mesmo volume!
Resposta
Três opções de integrais para calcular aquele volume são , e .