3) Arraste e solte, nos campos correspondentes, o valor correto de cada elemento, conforme as opções disponíveis.
a) onde:
e
Passo 1
Falaaa... beleza??
Nessa questão vamos precisar mudar a ordem de integração dessa integral tripla.
Pra isso, vamos desenhar a região de integração (que são os limites das integrais de dentro) e trocamos a ordem.
Repara que o continua na mesma posição (mais pra fora) da integral nas duas integrais triplas. Então nem precisamos mexer nele.
Já podemos responder que e .
Passo 2
Com variando de até 1 e com variando de até . Temos:
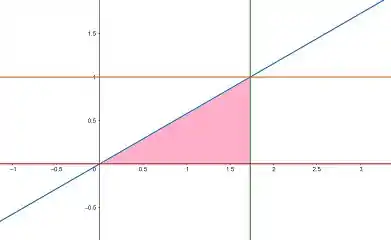
E pra mudar a ordem de integração temos que o vai variar de onde a reta azul, que é a equação , cruza com a reta vermelha (reta ) :
Até onde a reta azul cruza com a reta verde e a laranja:
Passo 3
Para o , temos que ele varia da reta vermelha:
Até a reta inclinada:
Como não tem nenhuma mudança de variáveis, então o que a gente está integrando não muda... A integral fica: