Calcule a integral, mudando a ordem de integração de forma apropriada
Passo 1
Assim como aconteceu no exemplo da teoria, vemos que não conseguiríamos integrar direto em função de . Portanto, vamos ter que integrar alguma outra variável antes, certo?
Vamos antes entender o nosso sólido:
Esboçando esses limites temos:
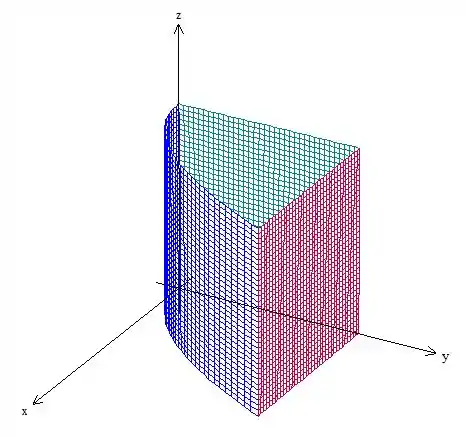
Passo 2
Como não queremos integrar em , vamos mudar a ordem de integração para
No plano , tínhamos limitado por
E limitado por
No plano :
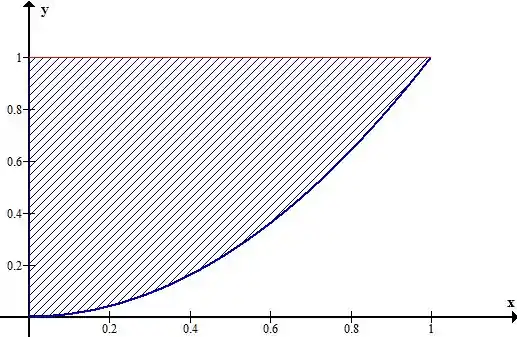
Invertendo a ordem de integração:
Como temos que é positivo, vamos pegar somente a raiz positiva
Os limites de continuam os mesmos:
Passo 3
Reescrevendo a integral:
Passo 4
Integrando em :
Para integrar em , vamos fazer a substituição
Os limites em ficam:
Temos então a integral:
Integrando em :
Integrando em :