Calcule a integral:
Mudando a ordem de integração de maneira apropriada.
Passo 1
Vamos ver se podemos simplificar um pouco essa integral antes de resolver.
O não aparece em nenhum dos limites de integração, e a função e que ele aparece é bastante simples de integrar.
Então vamos começar integrando em relação a . Nesse caso, podemos pensar em todos os outros fatores da função como constantes, e colocá-los “para fora” da integral:
A integral de é , então:
Lembrando que , e também que , obtemos:
E então nossa integral vira:
Agora sim, vamos tentar inverter a ordem de integração.
Passo 2
O primeiro passo para inverter a ordem de integração é desenhar a região no plano .
Nesse caso, o eixo horizontal vai representar o . Na integral original, ele varia nesse intervalo:
E para cada um desses valores de , o varia entre as funções e :
Vamos desenhar isso no plano:
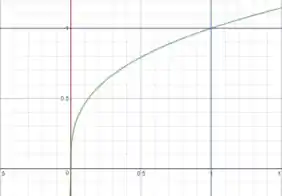
Para inverter a ordem de integração, vamos mudar a situação original. Agora o vai ser limitado por constantes:
E para cada ponto nesse intervalo, o (que está no eixo horizontal), vai desde o até a função , ou , ou seja:
Então nossa integral fica assim:
Passo 3
Ótimo, agora como o não aparece em nenhum limite de integração ou na função, podemos escrever essa integral da seguinte forma:
E como aquele integral entre parênteses resulta em , obtemos o seguinte:
Beleza, agora vamos tentar usar uma substituição:
E os novos limites de integração serão:
Então:
Agora precisamos dar um jeito naquele , vamos escrever ele em função do :
Então:
Beleza, agora temos uma integral bem mais razoável.
Passo 4
Para simplificar, vamos tentar simplesmente achar a integral indefinida, e depois colocamos as constantes e os limites de integração:
Lembra da fórmula para integração por partes?
Se chamarmos e , então e , jogando isso na fórmula:
E integrando por partes de novo para encontrar aquela segunda integral. Vamos chamar e , então e
Jogando isso na equação anterior:
Então a integral que queríamos calcular desde o início dá:
Passo 5
Agora que sabemos a integral indefinida, vamos concluir a questão:
Como , , , , então:
Pronto! A essa altura pode até parecer muito distante, mas esse é o valor daquela integral tripla do enunciado!
Resposta
O valor da integral é