O fabricante de determinado modelo de automóvel afirma que seu desempenho médio é de de gasolina. Testes foram feitos em 36 desses veículos, escolhidos ao acaso, e apurou-se um desempenho médio de . Admita que o desempenho siga o modelo Normal com variância igual a . Através do p-valor execute os dois testes, itens (a) e (b) a seguir, com relação a afirmação do fabricante:
(a) contra a alternativa . Que decisão deve ser tomada ao nível de 5%?
(b) contra a alternativa . Que decisão deve ser tomada ao nível de 5%?
(c) No item (a) obtenha a região de rejeição com . Se, de fato, , isso corresponderia a que valor da probabilidade do erro tipo II?
Passo 1
a)
Vamos começar expondo as hipóteses que o enunciado pediu para testarmos:
“Aiii, mas comé que faz teste com sinal de na hipótese nula???” Relaaaxa, nosso teste vai ser feito exatamente da mesma forma. Escreve assim porque foi pedido pelo enunciado, mas não se preocupa que nossa resolução vai ser a mesma.
Então estamos num teste unilateral inferior para média.
Passo 2
Nossa estatística de teste é dada por:
Pelo enunciado, conseguimos identificar todos esses caras aí da fórmula. Substituindo:
Agora calculamos nosso P-valor. No unilateral inferior, ele é dado por:
Mas desse jeito não conseguimos achar nosso na tabela da Normal, temos que tirar esse negativo. Para isso, invertemos o sinal de :
Mas agora entramos no problema do sinal , a nossa tabela dá valores para ! Então vamos trabalhar com a probabilidade complementar:
Procurando na tabela...
Então esse aí é o nosso P-valor. No enunciado, podemos ver que nosso nível de significância , daí temos que:
Passo 3
b)
Agora temos a mesma coisa que anteriormente com o porém do novo P-valor. Como nossa hipótese alternativa tem o sinal de , estamos num teste bilateral.
No teste bilateral, o P-valor é dado por:
Nosso continua a mesma coisa, ou seja, . Então:
E nós já calculamos essa probabilidade no item anterior:
Como nosso nível de significância , temos que:
E quando isso acontece, nós não rejeitamos a hipótese nula!
Passo 4
c)
Para calcular a região de rejeição (ou crítica) do nosso teste unilateral inferior, temos que calcular nossos pontos críticos.E nesse tipo de teste, ele é dado por:
Mas a gente usa esse ponto para comparar com a nossa estatística de teste, que é padronizada, certo? E quando a gente padroniza, os nossos valores dos parâmetros mudam e não são mais valores reais do problema, por que nós subtraímos e dividimos tudo por :
Então, se o nosso valor de não é o valor real, e a gente compara esse cara com o , isso provavelmente significa que o também não é real! E é justamente isso, o é um falor padronizado, que nem o .
Mas aqui nós queremos comparar diretamente com o valor , que não é um valor padronizado. Então vamos “despadronizar” o fazendo as operações inversas da padronização: ao invés de subtrair e dividir por , vamos multiplicar por e somar :
Vamos calcular o valor de cada termo dessa equação então, lembrando que :
Lembrando que esse é o que estamos testando, não necessariamente o real! Ou seja, é o que usamos para escrever as hipóteses.
Juntando todos esses valores, temos o nosso ponto crítico:
Passo 5
Agora que temos o ponto crítico, basta lembrarmos que, num teste unilateral inferior como é o nosso caso aqui, a região crítica é dada por tudo que está abaixo do ponto crítico. Então:
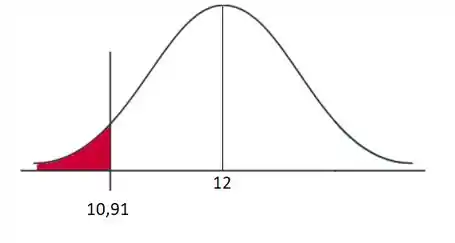
Passo 6
Erro de tipo II é quando não rejeitamos , mas é falsa. A probabilidade desse erro acontecer é:
No nosso caso, o enunciado diz que o valor verdadeiro de é . Então:
Calculando isso:
Resposta
a)
Rejeitamos a hipótese nula.
b)
Não rejeitamos a hipótese nula.
c)