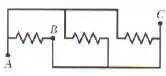
A figura abaixo mostra três resistores de . Determine a resistência equivalente
- entre os pontos A e B;
- entre os pontos A e C;
- entre os pontos B e C;
Passo 1
Essa questão é bem famosinha. Várias faculdades colocam ela em listas de exercícios. A princípio ela se parece esquisita mas jajá você vai ver que ela é simples.
Presta bem atenção!
Perceba que acima do ponto A até chegar no último resistor da direita não nada entre eles. Isso significa que eles são pontos equipotenciais, ou seja, com mesmo potencial.
A mesma coisa podemos dizer para o fio que sai de B e vai pra C. Não tem nada entre eles, então podemos dizer que o potencial de B é igual ao potencial em C.
Passo 2
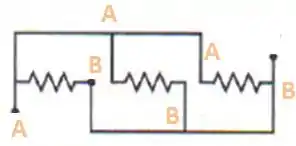
E mais,como vou mostrar na figura abaixo, a gente vai poder ver que todos os três resistores estão ligados entre A e B.
Saca só!
Passo 3
Podemos redesenhar o nosso circuito de uma forma bem melhor.
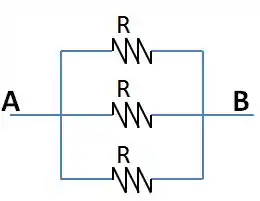
Agora ficou fácil,né?
Passo 4
b)
Como a gente já viu que o ponto B e o ponto C são os mesmo, a resistência equivalente vai ser igual, logo:
Passo 5
C)
Se o ponto B e C são os mesmos, significa dizer que não tem nenhuma resistência entre eles, logo: