Um fio de cobre , de e diâmetro de , está soldado em uma de suas extremidades a um fio de ferro de e mesmo diâmetro. A corrente nos fios é .
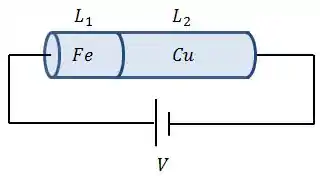
Calcule:
A densidade de corrente em cada fio;
O campo elétrico em cada fio;
A diferença de potencial em cada fio;
a resistência que é atravessada pela corrente de , sob a diferença de potencial total . Compare esta resistência com a resistência equivalente dos dois fios (justificar);
Passo 1
A densidade de corrente em cada fio;
Por definição, a densidade de corrente é dada por:
Onde corresponde à área transversal do fio.
Se os dois resistores possuem o mesmo diâmetro , possuem também a mesma área transversal, dada por:
Assim, a densidade de corrente será dada por:
Passo 2
O campo elétrico em cada fio;
O campo elétrico pode ser encontrado a partir da relação:
Então só precisamos pegar a resistividade de cada material:
Passo 3
A diferença de potencial em cada fio;
A diferença de potencial em cada fio será dada por:
Onde é o comprimento do fio. Portanto:
Passo 4
A resistência que é atravessada pela corrente de , sob a diferença de potencial total . Compare esta resistência com a resistência equivalente dos dois fios (justificar);
A diferença de potencial total será dada por:
A resistência atravessada pela corrente é:
Beleza! O nosso trabalho agora é calcular a resistência equivalente dos dois fios.
Passo 5
Nesse tipo de problema, o segredo é olhar pra ele como dois resistores em série. Assim, a resistência entre as extremidades da barra será:
A resistência é dada por:
Então vamos começar calculando as resistências desses caras, só temos que tomar cuidado com as unidades de medida:
Agora sim!
Portanto, a resistência entre as extremidades será:
A resistência equivalente dos dois fios é igual à resistência atravessada pela corrente de . Isso acontece porque a corrente deve, necessariamente, atravessar os dois fios (ferro e cobre), um após o outro, como se estivesse atravessando dois resistores em série.
Assim, as duas resistências calculadas devem ser igual porque são duas formas de calcular uma mesma resistência.
Resposta