Exercícios de Estabilidade de sistemas discretos - Lista de Exercícios Resolvida
Questão 1
Determine a faixa de ganho, , para tornar o sistema mostrado na figura abaixo estável.
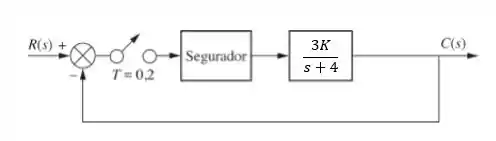
Questão 2
Determine a faixa de período de amostragem, , que tornará o sistema mostrado abaixo estável.
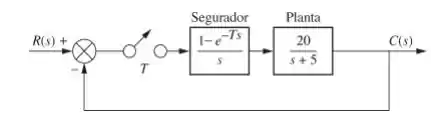
Questão 3
Determine a faixa de período de amostragem, , que tornará o sistema mostrado abaixo estável, e a faixa que o tornará instável.
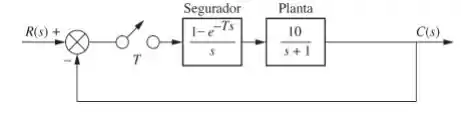
Questão 4
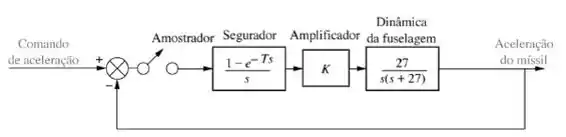
O míssil mostrado na figura abaixo pode ser controlado aerodinamicamente através de torques gerados pela deflexão de superfícies de controle no corpo do míssil. Os comandos para defletir essas superfícies de controle vêm de um computador que utiliza dados de rastreamento em conjunto com equações de guiamento programadas paradeterminar se o míssil segue a trajetória. As informações provenientes das equações de guiamento são utilizadas para desenvolver comandos de controle de voo para o míssil. Um modelo simplificado é mostrado abaixo. Nesse caso o computador executa a função de controlador utilizandoas informações de rastreamento para desenvolver comandos de entrada para o míssil. Um acelerômetro no míssil detecta a aceleração real, a qual é realimentada para o computador. Obtenha a função de transferência digital em malha fechada para esse sistema e determine se o sistema é estável para período de amostragem .
Questão 5
Dado , em que utilize o critério de Routh-Hurtwitz para determinar o número de polos de dentro, fora e sobre o círculo unitário. O sistema é estável?
Ver solução completaQuestão 6
Dado , em que utilize o critério de Routh-Hurtwitz para determinar o número de polos de dentro, fora e sobre o círculo unitário. O sistema é estável?
Ver solução completa