Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Superposição

Ver Teoria
Exercício 41235678910

Enunciado

Use superposição para determinar v x no circuito abaixo.

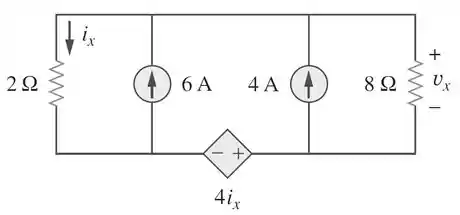
Passo 1

Precisamos encontrar v x utilizando o princípio da superposição. No circuito existem duas fontes independentes de corrente e uma fonte dependente de tensão.

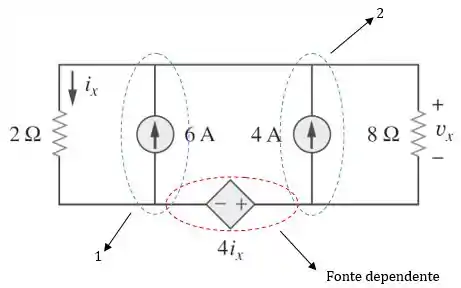
Logo, a tensão v x será a soma das contribuições de tensão das duas fontes independentes individualmente, ou seja:

v x = v 1 + v 2

Passo 2

Primeiro, vamos determina v 1 . Para isso, vamos desligar a fonte de corrente de 4   A , substituindo por um circuito aberto:

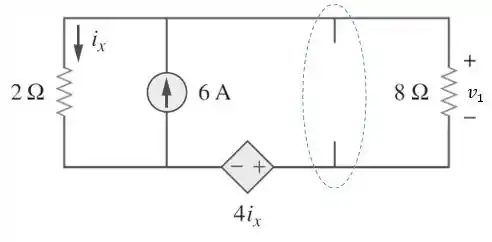
Passo 3

Vamos ajeitar o circuito e calcular a contribuição da fonte de tensão de 6   A , utilizando análise nodal.

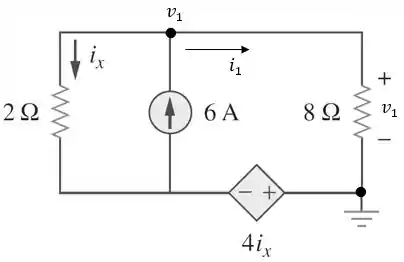
Aplicando a LCK no nó da tensão nodal v 1 :

i x + i 1 = 6

Passo 4

Escrevendo as correntes em função da tensão nodal:

i x = v 1 - ( - 4 i x ) 2         →       i x = - v 1 2

i 1 = v 1 8

Substituindo na equação das correntes do nó:

- v 1 2 + v 1 8 = 6

- 4 v 1 + v 1 = 48

- 3 v 1 = 48

v 1 = - 48 3   V

Passo 5

Falta determinarmos v 2 . Para isso, vamos desligar a fonte de corrente de 6   A , substituindo por um circuito aberto.

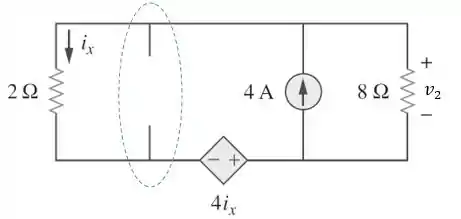
Passo 6

Agora, vamos ajeitar o circuito e calcular a contribuição da fonte de tensão de 4   A , utilizando análise nodal.

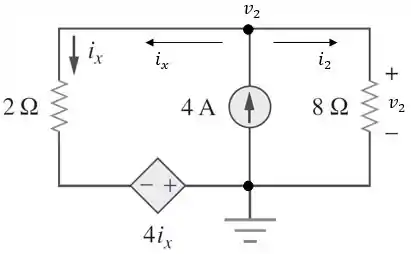
Aplicando a LCK no nó da tensão nodal v 2 :

i x + i 2 = 4

Passo 7

Escrevendo as correntes em função da tensão nodal:

i x = v 2 - ( - 4 i x ) 2         →       i x = - v 2 2

i 2 = v 2 8

Substituindo na equação das correntes do nó:

- v 2 2 + v 2 8 = 4

- 4 v 2 + v 2 = 32

- 3 v 2 = 32

v 2 = - 32 3   V

Passo 8

Agora é somar as contribuições e correr para o abraço:

v x = v 1 + v 2

Substituindo:

v x = - 48 3 + - 32 3

v x = - 80 3 = - 26,667   V

Resposta

v x = - 26,667   V

Exercícios de Livros Relacionados

10. Usando a figura 4.78 elabore um problema para ajudar outros estudantes a entenderem melhor o teorema da superposição. Note que a letra k é um ganho que você pode especificar de forma a tornar o pr
8. Usando a superposição, determine V 0 no circuito da Figura 4.76 . Confira usando o P s p i c e ou o M u l t i S i m .
9. Dado que I = 4A quando V s = 40V e I s = 4A e I = 1A quando V s = 20V e I s = 0A , use o teorema da superposição e linearidade para determinar o valor de I quando V s = 60V e I s = - 2A .
14. Aplique o princípio da superposição para determinar v 0 no circuito da figura 4.82
16. Dado o circuito da figura 4.84 , use superposição para obter i 0 .