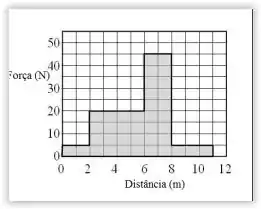
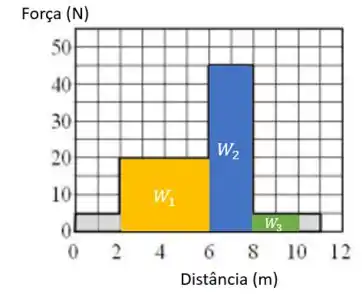
O gráfico mostra a componente de uma força aplicada a um corpo ao longo do deslocamento como uma função da magnitude do deslocamento. Determine o trabalho realizado pela força durante o intervalo de a .
(A)
(B)
(C)
(D)
(E)
Passo 1
Bom, pessoal, quando temos um gráfico , a área do gráfico é o próprio trabalho realizado pela força.
Então só precisamos achar a área do gráfico, mas presta atenção de uma coisa, o enunciado deixou bem claro que ele quer o trabalho entre e , sendo que o gráfico mostra entre e , então temos que cortar o pedaço que queremos:
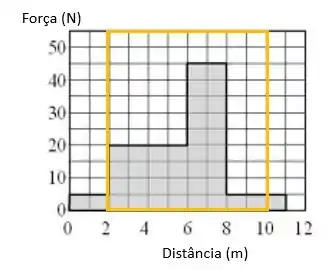
Passo 2
Perceba que de até , temos a mesma força igual a formando um retângulo:
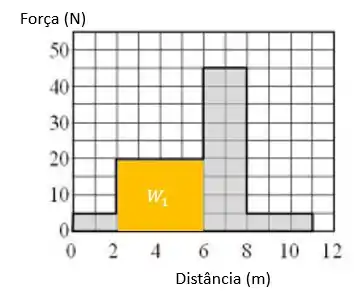
Então o trabalho nesse percurso será igual a área do retângulo:
A nossa base é o intervalo de metros percorridos:
Enquanto a altura será o intervalo de força:
Colocando na fórmula da área:
Encontramos a primeira parcela do trabalho total! Vamos para o segundo intervalo:

Como também se trata de um retângulo, o trabalho nesse percurso será igual a área do retângulo:
A nossa base é o intervalo de metros percorridos:
Enquanto a altura será o intervalo de força, veja que a força está exatamente no meio entre e , logo, vamos considerar que será :
Colocando na fórmula da área:
Encontramos a segunda parcela do trabalho total! Vamos para o terceiro e último intervalo:
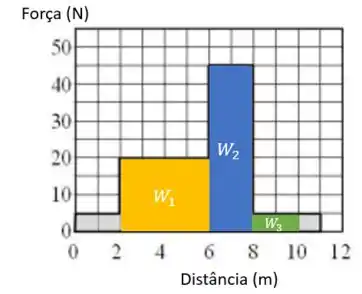
Outro retângulo:
A nossa base é o intervalo de metros percorridos:
Enquanto a altura será o intervalo de força, veja que a força está exatamente no meio entre e , logo, vamos considerar que será :
Colocando na fórmula da área:
Passo 3
O trabalho total é a soma dos trabalhos parciais , e :
Substituindo os valores que encontramos:
Pronto, o trabalho total é igual a , esse era o resultado que buscávamos e que é representado pela letra “B”.
Resposta
(B)