Sejam e . Encontre
Passo 1
Show galerinha, nessa questão nós temos mais operações a serem feitas, mas o procedimento é o mesmo!!
Primeiro de tudo, vamos colocar os vetores na forma matricial. Pra isso, nós construímos uma matriz coluna com cada linha correspondendo a uma coordenada do nosso vetor. Assim teremos as matrizes:
Beleza, agora vamos começar a resolver.
Passo 2
A questão está querendo que a gente faça:
Mas antes de substituir as matrizes que encontramos nessa expressão, vamos organizá-la um pouquinho! Podemos ver que o está multiplicando o que está dentro dos parênteses, então vamos resolver essa multiplicação fazendo uma distributiva:
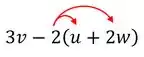
Agora sim, vamos substituir as matrizes correspondentes aos vetores , e nessa expressão:
Multiplicamos cada elemento da matriz pelo que está de fora:
E teremos:
Agora, o que nos resta é realizamos as operações. Como são subtrações, podemos criar uma nova matriz resultante onde os elementos serão o resultado das operações realizadas com os elementos que estavam na mesma posição:
![]()
Resolvendo as operações de cada linha, encontramos nossa resposta:
Legal, não foi?