A figura abaixo mostra um ciclo ao qual uma porção de gás ideal monoatômico é submetida. O ciclo é composto por três etapas: um processo onde a pressão varia linearmente com o volume (), um processo isocórico () e um processo isobárico ().
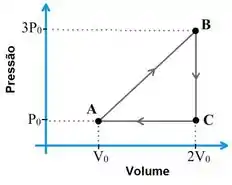
Escrevendo todas as suas respostas apenas em termos de e , faça o que é pedido abaixo.
- Determine o trabalho realizado e o calor recebido pelo gás em cada uma das três etapas
- Qual é a eficiência da máquina que opera com o ciclo da figura acima? Se uma máquina de Carnot operasse entre a máxima e mínima temperatura do ciclo da figura acima, qual seria a eficiência da máquina de Carnot?
Passo 1
No diagrama o trabalho é dado pela área abaixo da curva que representa o processo, sendo positivo para expansão (aumento de volume) e negativo para compressão (diminuição de volume).
A energia interna de um gás ideal monoatômico é dada por
Usando a equação dos gases ideais , temos
De forma que a variação de energia interna em um processo é dada por
Assim usando a primeira lei da termodinâmica podemos calcular o calor recebido pelo gás
Passo 2
-
Temos aqui que a área de baixo da curva é a área de um trapézio (deitado) de base menor , base maior e altura . O trabalho será essa área com sinal de , pois estamos falando de uma expansão
Já a variação de energia interna é dada por
Assim o calor recebido é dado por
Passo 3
-
Aqui temos um processo isovolumétrico, ou seja o trabalho é nulo
Já a variação de energia interna é dada por
E o calor recebido é dado por
Passo 4
-
Temos aqui que a área de baixo da curva é a área de um retângulo de base e altura . O trabalho será essa área com sinal de , pois estamos falando de uma contração.
A variação de energia interna é dada por
Assim o calor recebido é dado por
Passo 5
A eficiência do ciclo é dada por
Temos que o trabalho do ciclo é dado por
Já o calor recebido é dado por todas contribuições positivas para o calor total (contribuições negativas são calor perdido). Como o calor recebido só é positivo no processo , temos
Assim, a eficiência é dada por
Passo 6
Temos que a temperatura máxima do ciclo acontecerá no ponto
E a temperatura mínima acontecerá no ponto
A eficiência de um ciclo de Carnot operando nessas temperaturas é dada por
Resposta
(a)
(b) e