Uma máquina térmica funciona seguindo o ciclo mostrado na figura abaixo. A substância de trabalho é de gás hélio (monoatômico), considerado ideal, o qual atinge uma temperatura máxima de . O processo é isotérmico. A pressão nos estados e vale , e a pressão no estado vale .
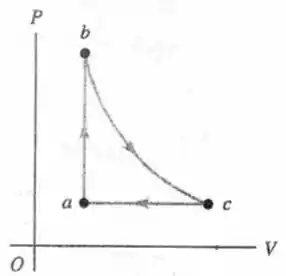
Encontre a quantidade de calor que o gás recebe em cada um dos trechos, indicando o seu sinal (positivo quando calor entra e negativo quando sai).
Qual o trabalho total realizado pelo gás no ciclo?
Qual a eficiência dessa máquina?
Suponha que essa máquina opere com uma fonte quente e outra fria. Qual a temperatura mínima, , que deve ter a fonte quente? Qual a temperatura máxima, , que deve ter a fonte fria? Explique.
Qual a razão entre a eficiência dessa máquina e a máxima eficiência possível para uma máquina que opera entre as mesmas temperaturas, e .
Justifique as respostas.
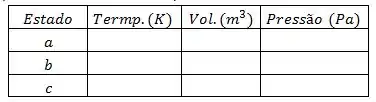
(dica: pode ser útil preencher a tabela abaixo)
Passo 1
Na teoria vimos que para cada processo temos um meio de calcular a quantidade de calor.
Então vamos determinar o tipo de processo em cada etapa para podemos saber qual fórmula de quantidade de calor usar.
O processo mantem o volume, então é isovolumétrico. E por isso calculamos a quantidade de calor por:
Onde vale porque o gás é monoatômico.
O processo é isotérmico, e por isso a variação da energia interna é zero. E pela primeira lei da termodinâmica, temos:
E a fórmula de trabalho em um processo isotérmico foi dada pela questão
Já o processo é isobárico, ou seja, mantem a pressão constante. E por isso a quantidade de calor é dada por:
Lembrando que , então irá valer
Passo 2
A dica da questão ainda fala em preenchermos a tabela, a tabela irá concentrar as informações que teríamos que descobrir ao longo da questão para resolvê-la.
Então, vamos ver os dados que já temos dessa tabela. O enunciado nos deu as pressões. E a temperatura máxima.
A temperatura máxima é , essa é a temperatura dos pontos e , pois pelo gráfico vemos que a isoterma em que eles estão está acima da isoterma que está.
Bom, ainda temos que encontrar a temperatura que temos em e para isso vamos usar ”PiViTi-PoVoTo”:
Por que vamos fazer isso entre os estados e ? Primeiro porque queremos a temperatura em , então o estado tem que estar incluso, e escolhemos , porque o processo é isovolumétrico, então não precisamos saber o volume e isso é essencial, porque realmente não temos o volume dos estados.
Como temos a temperatura em graus Celsius, temos que transforma-la em Kelvin, por isso somamos ela a
Agora temos as pressões e temperaturas, falta apenas os volumes. Mas tendo temperatura, numero de mols e pressão fica mole achar o volume. Só usar a equação geral dos gases.
O volume no estado é o mesmo que no estado , então:
Agora, vamos encontrar o volume em . Analogamente ao que fizemos para calcular o volume em :
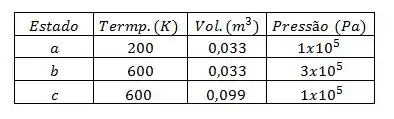
A tabela preenchida ficou assim:
Passo 3
Agora, podemos voltar ao item e calcular a quantidade de calor de cada etapa, começando pelo processo :
Como já vimos, a quantidade de calor será dada por:
A quantidade de calor no processo , será igual ao trabalho e será dada por:
E no último processo ” a quantidade de calor é:
Passo 4
O trabalho total é a soma do trabalho de cada processo
Como o processo é isovolumétrico, então o trabalho é zero, pois o volume não varia.
O trabalho do processo já calculamos e ele vale:
Só falta descobrirmos o valor do trabalho do processo . Como vimos na teoria o trabalho tem módulo igual a área sobe a curva que descreve o caminho do processo. E o sinal é o mesmo que o da variação de volume, que nesse caso é negativo.
Temos a área, assim o trabalho será:
O trabalho total será soma do trabalho de cada processo e por isso:
Passo 5
A eficiência de uma máquina térmica é dada pela razão do trabalho total pela quantidade de calor absorvida pelo gás.
O trabalho total nós terminamos de encontrar no item , e no item encontramos o calor transferido em cada processo, sendo sinal positivo o calor absorvido e sinal negativo o calor cedido pelo gás.
Assim, termos que a eficiência é dada por:
Passo 6
O enunciado nos forneceu a temperatura máxima desse ciclo certo? e a gente calculo a temperatura no ponto e pelo gráfico que esse ponto é o ponto que passa a menor isoterma do ciclo, sendo assim a menor temperatura .
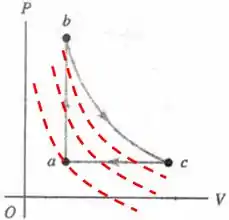
De vermelho temos algumas isotermas, mostrando que é a temperatura mínima desse ciclo.
Vamos ao que a questão pediu agora, ela quer a mínima temperatura quente que esse ciclo pode operar. Como o próprio nome diz: temperatura quente, é a temperatura da fonte de calor, que vai emitir calor. Então será , pois essa é nossa temperatura máxima, se fosse menor que , teria algum momento que a fonte que deveria fornecer calor iria receber, pois o nosso ciclo opera até , então a temperatura quente não pode ser menor que a nossa máxima temperatura.
E a máxima temperatura fria que poderíamos ter? A temperatura fria é a temperatura da fonte que recebe calor, e por isso ela deve ser no máximo , pois se ela tivesse temperatura maior que , quando o sistema atingisse a temperatura mínima que ele opera a fonte que deveria apenas receber calor estaria emitindo. Por isso a máxima temperatura de é .
Passo 7
A máxima eficiência de uma máquina térmica é quando essa máquina opera pelo ciclo de Carnot. E a eficiência no ciclo de Carnot é dada por:
A questão quer saber a razão entre a eficiência da nossa máquina (encontramos essa eficiência no item ) pela eficiência máxima possível para essas temperaturas (foi o que terminamos de calcular).
Assim a razão desejada é:
Resposta