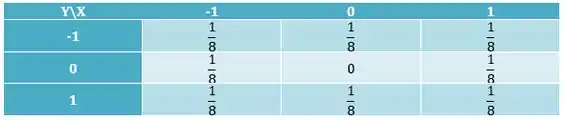
O exemplo a seguir ilustra que não implica independência. Suponha que (X,Y) tenha distribuição conjunta dada pela tabela abaixo.
a) Mostre que E(XY)=E(X)E(Y), donde
b) Justifique por que X e Y não são independentes.
Passo 1
a) Mostre que E(XY)=E(X)E(Y), donde
Sabemos que
Então
Passo 2
Vamos calcular agora E(X) e E(Y):
Assim
Passo 3
Comparando, temos
Como querímos demonstrar.
Passo 4
b) Justifique por que X e Y não são independentes.
Uma forma de verificar se X e são independentes ou não é verificando se
Temos que testar TODAS as possibilidades. Se apenas uma não for válida podemos dizer que elas não são independentes. Pela tabela fica beeem mais tranquila a visualização.
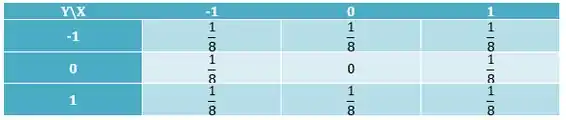
Vamos direto no , pois este vale 0 então é alta a chance de ele falhar.
Como podemos afirmar que X e Y não são independentes.
Resposta
Ei, a resposta está no passo a passo :)