Exercícios de Covariância e Correlação para V.a. Multidimensionais - Lista de Exercícios Resolvida

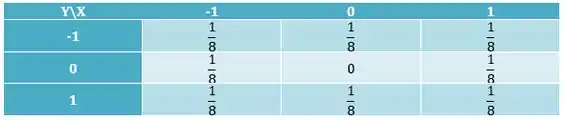
O exemplo a seguir ilustra que não implica independência. Suponha que (X,Y) tenha distribuição conjunta dada pela tabela abaixo.

a) Mostre que E(XY)=E(X)E(Y), donde

b) Justifique por que X e Y não são independentes.

b) Mostre que o coeficiente de correlação é igual a 1 quando e .

Uma urna contém 3 bolas brancas e 2 bolas vermelhas. Um experimento consiste em se extrair sequencialmente e sem reposição duas bolas e registrar suas cores. Seja a v.a. que representa o número de bolas brancas retiradas nas duas extrações e seja a v.a. que assume 1 se a primeira bola extraída é branca e 0 se a primeira bola extraída é vermelha.

1. Obtenha a distribuição conjunta de e através de uma tabela e diga se e são independentes, justificando. Sugestão: Na montagem da tabela, comece determinando as distribuições marginais de e de . Em seguida, obtenha e . Finalmente complete a tabela, respeitando as propriedades de uma distribuição conjunta.
2. Calcule a covariância de e .

Considerando a população dos profissionais à busca de emprego em uma certa fatia do mercado de trabalho, há duas habilidades consideradas importantes para se ter sucesso: dominar o Inglês e dominar a Informática. Sabe-se que:

1. a proporção de profissionais que dominam o Inglês é igual a proporção de profissionais que dominam a Informática (denote por essa proporção comum às duas habilidades);
2. o número médio de habilidades por profissional é 1,4;
3. a variância desse número de habilidades por profissional é 0,24.

Calcule:

1. o valor de;
2. o coeficiente de correlação entre dominar o Inglês e dominar a Informática
3. a proporção de profissionais que possuem ao mesmo tempo as duas habilidades.

Sugestão: Defina as variáveis aleatórias.

Considere a distribuição conjunta das variáveis aleatórias a seguir.

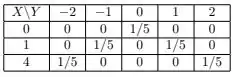
Pode-se afirmar sobre :

a) ;

b) ;

c) , logo são independentes ;

d) São dependentes.

Uma urna contém 3 bolas brancas e 2 bolas vermelhas. Um experimento consiste em se extrair sequencialmente e sem reposição duas bolas e registrar suas cores. Seja a v.a. que representa o número de bolas brancas retiradas nas duas extrações e seja a v.a. que assume 1 se a primeira bola extraída é branca e 0 se a primeira bola extraída é vermelha.

1. Obtenha a distribuição conjunta de e através de uma tabela e diga se e são independentes, justificando. Sugestão: Na montagem da tabela, comece determinando as distribuições marginais de e de . Em seguida, obtenha e . Finalmente complete a tabela, respeitando as propriedades de uma distribuição conjunta.
2. Calcule a covariância de e .

Duas roletas idênticas, que podem resultar nos números e com igual probabilidade, serão colocadas para rodar simultaneamente. Nesse contexto, defina as seguintes variáveis:

Menor número observado entre os resultados das duas roletas.

Maior número observado entre os resultados das duas roletas.

1. Construa a tabela da função de probabilidade conjunta de e .
2. Obtenha a distribuição condicional de dado .
3. Calcule a variância de .

Considere a distribuição conjunta das variáveis aleatórias e , parcialmente dada pela seguinte tabela:

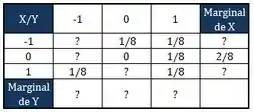
1. Sabendo que , complete a tabela.
2. Calcule e .
3. As variáveis e são independentes?
4. Quando um exemplo pode ser usado para se mostrar que uma afirmação do tipo (SE... ENTÃO...) é falsa então dizemos que ele é um contra-exemplo para essa afirmação. Os itens anteriores constituem um contra-exemplo para que afirmação falsa?

Um jovem casal deseja ter dois filhos. Analisando as condições do casal, o médico afirma que a probabilidade deles terem dois meninos é de 40% e que a chance do primeiro bebê a nascer ser menina é 50%. O médico também informou que se o primeiro filho for menina, a probabilidade condicional do segundo ser menina é de 40%. Denotem as variáveis aleatórias por , se o bebê for menino e , se o bebê for menina no i-ésimo nascimento . Encontre:

1. A distribuição de probabilidade conjunta de e com suas distribuições de probabilidades marginais.
2. A probabilidade do segundo filho do casal também ser um menino, dado que o primeiro foi um menino.
3. A covariância entre e .

Considerando a população dos profissionais à busca de emprego em uma certa fatia do mercado de trabalho, há duas habilidades consideradas importantes para se ter sucesso: dominar o Inglês e dominar a Informática. Sabe-se que:

1. a proporção de profissionais que dominam o Inglês é igual a proporção de profissionais que dominam a Informática (denote por essa proporção comum às duas habilidades);
2. o número médio de habilidades por profissional é 1,4;
3. a variância desse número de habilidades por profissional é 0,24.

Calcule:

1. o valor de;
2. o coeficiente de correlação entre dominar o Inglês e dominar a Informática
3. a proporção de profissionais que possuem ao mesmo tempo as duas habilidades.

Sugestão: Defina as variáveis aleatórias.

b) Mostre que o coeficiente de correlação é igual a 1 quando e .

Qual a relação entre Correlação e Independência entre duas ou mais variáveis?

Sejam e v.a.’s contínuas com densidade conjunta:

1. Encontre a constante que faz desta expressão uma densidade.
2. Encontre a densidade marginal de .
3. Encontre a densidade marginal de .
4. Encontre a densidade condicional de dado .
5. e são independentes? Por que? Justifique.

b) Seja variável aleatória discreta com a seguinte distribuição de probabilidade conjunta:

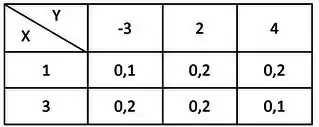
Pede-se:

Calcular e o Coeficiente de Correlação

Observação:

- Demonstrar a expressão da Covariância.

- Mostre os resultados considerando 4 casas decimais.

b) Mostre que o coeficiente de correlação é igual a 1 quando e .

Sejam e variáveis aleatórias discretas com a seguinte função de probabilidade conjunta:

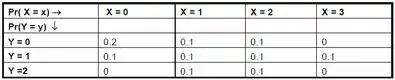
Pede-se:

Calcular a covariância de e , , e o coeficiente de correlação detalhando seus passos para a obtenção de cada termo.

Sejam e v.a. contínuas com densidade conjunta:

Pede-se:

1. A marginal de e de .
2. Densidade condicional de dado .
3. Média condicional de dado .
4. Variância condicional de dado .

A partir de uma variável aleatória uniformemente distribuída sobre o intervalo , defina duas variáveis aleatórias e da seguinte maneira:

(a) Obtenha a função de probabilidade conjunta do par .

(b) As variáveis aleatórias e são independentes? Justifique.

(c) Calcule .

(d) Calcule e .

Calcular o coeficiente de correlação entre e para o caso em que . Mostre todos os passos para se chegar ao resultado final partindo do coeficiente de correlação de e .

Sejam e duas v.a.’s discretas cuja função de probabilidade conjunta é expressa por:

1. Constante para que para que seja uma função de probabilidade das variáveis aleatórias e .
2. Densidade condicional de dado .
3. Podemos afirmar que e são independentes? Justifique sua resposta.

Determine a constante para que seja uma função de probabilidade das variáveis aleatórias e .

Seja um vetor aleatório bivariado com a seguinte função de densidade de probabilidade conjunta:

Pede-se: calcular o coeficiente de correlação .

Observe-se:

- Mostre os resultados considerando 4 casas decimais.

Uma moeda equilibrada é lançada duas vezes. Uma cara é associada ao número 1 e uma coroa, ao número 0. O par de variáveis aleatórias é definido como:

resultado do primeiro lançamento + resultado do segundo lançamento

resultado do primeiro lançamento − resultado do segundo lançamento

(a) Encontre a função de probabilidade conjunta do par

(b) Encontre as distribuições marginais de e .

(c) Calcule a covariância entre e .

(d) e são independentes? Justifique sua resposta.

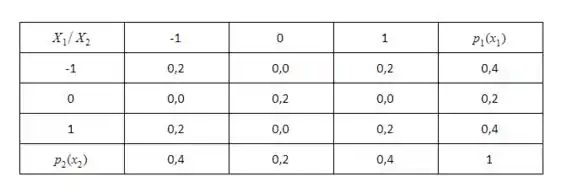Sejam (X1, X2) a variável aleatória bidimensional cuja distribuição conjunta é dada pela tabela:

(a) Calcule e , sendo.

(b) Calcule , e . As v.a.‘s e são independentes?

(c) O que se pode dizer sobre a veracidade da afirmação: "Se e são independentes, então "? Justifique.

(d) O que se pode dizer com relação a esta afirmação: "Se , então e são independentes"? Justifique

Qual a relação entre correlação e independência entre duas variáveis aleatórias?