UERJ, Sem Campus, Cálculo III, P1 - Profº Claudio Plínio - 2019.2, Questão 3b
Desenhar as curvas ou superfícies de nível dos seguintes campos escalares.
b)
Passo 1
Eaew, belezinha?
A questão pede para a gente calcular as curvas ou superfícies de nível da função f dada. Como f é uma função de 3 variáveis, temos que, quando fizermos uma de suas variáveis constante, obteremos uma função de duas variáveis que irá descrever uma superfície. Primeiramente, vamos dar uma olhada no gráfico de uma exponencial quadrática de uma função de uma variável, :
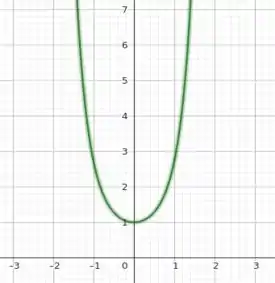
Temos que a função é sempre positiva e, se multiplicarmos por uma constante, teremos que a função será deslocada na vertical e se tornará mais estreita. Para duas variáveis, temos algo semelhante: como a função depende apenas da distância do ponto à origem, , temos que quando fizermos uma das variáveis constante, vamos ter superfícies com simetria axial. Então, bora lá esboçar as superfícies de nível!
Passo 2
Se fizermos z = k constante na equação da função f e considerando o eixo vertical como o eixo de f(x, y, z = k), obtemos uma função que se assemelha a um parabolóide de revolução e, conforme alteramos os valores de k, teremos fatores multiplicadores diferentes, como ilustra as figuras a seguir:
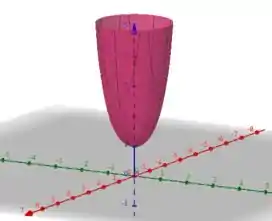
Semelhantemente, como as variáveis x,y e z contribuem todas da mesma forma para a função f(x,y,z), se fizermos x = k constante e consideramos o eixo vertical como o eixo da função f(x=k, y , z), teremos as mesmas superfícies de nível. A mesma coisa ocorre para y = k constante.
Por outro lado, se fizermos a própria função como constante, f(x,y,z) = k cte, podemos escrever a função como
Temos que as superfícies de nível correspondem a esferas com raios iguais à , pois
Resposta
Desenvolvida ao longo da questão.