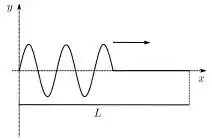
Uma corda de comprimento tem massa e está submetida a uma tração , com o extremo em preso a um suporte numa parede. Uma onda é produzida nesta corda ao movimentar-se seu extremo em num movimento harmônico com um período de . No instante esta extremidade da corda passava por com velocidade .
a) Calcule a velocidade de propagação , a frequência angular e o comprimento de onda da onda formada na corda.
b) Escrevendo a função de onda na forma , determine a amplitude e a constante de fase desta onda, antes que ela atinja o outro extremo em .
Onde aplicável, a resposta pode ficar em função de .
Passo 1
Para resolver a letra (a), vamos usar algumas fórmuletas 😊
Primeiro, vamos achar a velocidade. Para isso, podemos usar a fórmula da velocidade numa corda:
Onde , pois trata-se da densidade linear da corda. Substituindo na fórmula:
Passo 2
Além disso, temos que e o enunciado nos disse que , logo:
Passo 3
Para achar o comprimento de onda, temos a relação:
Passo 4
Na letra (b), o enunciado pede para usarmos a equação:
Utilizando o gráfico e a última informação do enunciado, podemos ver que:
Logo:
Passo 5
Mas e agora? Vamos usar ou ?
Bom, para responder isso, nós vamos olhar para a velocidade transversal dessa onda . Ou seja, podemos derivar em relação ao tempo e achar a velocidade no eixo :
Pelo enunciado, nós temos:
E, com isso:
Dessa forma, para que o termo fique negativo, o tem que ser negativo. Então:
Pela equação da velocidade ():
Agora, substituindo os valores de e :
Resposta
- ; ;
- ;