Para o campo de tensão bidimensional da figura abaixo sabe-se que:
Encontre as tensões de cisalhamento e normal que atuam sobre o plano de corte AA no elemento, a um ângulo de como mostra a figura.
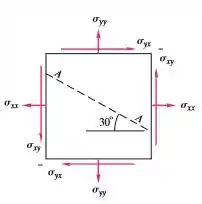
Passo 1
Queremos as tensões que irão atuar no elemento no plano de corte , então a primeira coisa que vamos fazer é desenhar o elemento cortado.
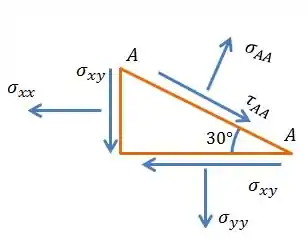
Para que o elemento não saia andando perdido pelo mundo o somatório de tensões deve ser zero, certo?
Bem, podemos fazer isso de duas formas, uma seria decompor as forças na direção do corte e a outra seria decompor as tensões na direção .
O mais fácil é decompor no plano do corte, assim podemos começar a fazer o sistema de equações para resolver o problema.
Passo 2
Então agora vamos fazer o sistema de equações na direção perpendicular ao corte . O somatório de forças nessa direção tem que ser zero, e nessa direção temos a ação da força normal e das outras tensões decompostas.
Então vamos começar a decompor as tensões, assumindo que está na direção positiva.
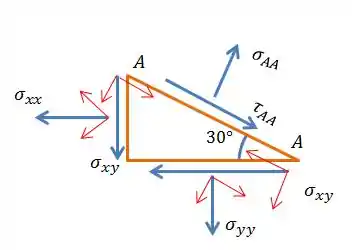
Só que a lei de Newton é sobre força e não pressão, então temos que multiplicar pelo comprimento do quadrado. O certo seria pela área, mas como a espessura é a mesma então cortamos ela e sobra só o comprimento, falou?
Confuso? Bem, olha a imagem abaixo, onde adotamos que o comprimento do corte é , assim o comprimento da lateral será e da base será .
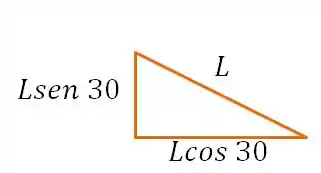
Multiplicando a tensão pelo comprimento do lado em que ela é aplicada temos:
Cortando e substituindo os valores dados no enunciado para descobrir temos:
Assim, o valor da tensão normal é:
Passo 3
Agora vamos equacionar na direção de cisalhamento:
Cortando o e substituindo os valores dados no enunciado para descobrir temos: