Abaixo é dada uma seção retangular de altura 40cm e base 20 cm. Sabendo que a seção somente suporta uma tensão cisalhante de no máximo 500Kpa, determine a que altura ocorreria a tensão cisalhante imediatamente anterior ao rompimento da mesma. Vale ressaltar que a peça está sofrendo a ação de um cortante de 200KN na direção mostrada.
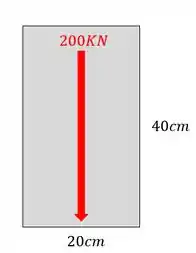
Passo 1
Para resolvermos essa questão precisamos analisar cada elemento da nossa fórmula a fim de descobrir em que ponto estará a nossa incógnita (que já sabemos de antemão que se trata da altura em que alcançamos o cisalhante admissível da nossa peça, que também já sabemos ser 80Mpa).
A nossa fórmula para cisalhamento é dada por
Em que sabemos que
= tensão cisalhante
= esforço cortante
= Momento Estático
= Momento de Inércia
= espessura do ponto que calculamos o cisalhante
Agora que já sabemos o que cada termo da nossa fórmula significa, vamos identificar cada um desses valores na nossa seção.
Passo 2
O primeiro passo é determinar a posição da linha Neutra. Como se trata de uma seção retangular, sabemos que a linha neutra passa no centro da nossa seção, como mostra a figura
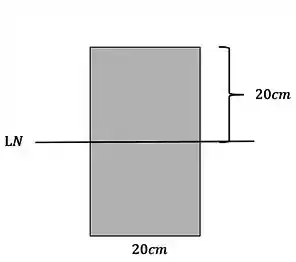
Também temos pelo enunciado dois valores
Um valor é o cortante
O outro valor é o próprio cisalhante
Passo 3
Também sabemos que devemos garantir o valor do momento de inércia, pois esse se trata diretamente do valor referente a seção, ou seja, independente do ponto em que calculamos o cisalhante.
Como se trata de uma seção retangular, sabemos que o momento de inercia será dado por
Como já vimos sabemos que
Substituindo teremos que
Também sabemos que a seção que iremos calcular tem espessura constante, que é o próprio valor de B, logo teremos que
Até aqui tudo bem, agora precisamos determinar o nosso momento estático.
Passo 4
Sabemos que a fórmula do momento estático é dada por
Em que é a área da seção acima do ponto em que estamos calculando o cisalhante e é o centroide que calculamos para essa área, porém em que ponto estamos calculando o cisalhante? Vamos ver a imagem abaixo para facilitar o entendimento.
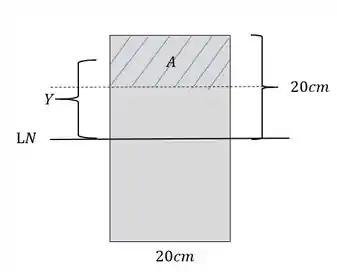
como não sabemos a altura em que o cisalhante ocorre, vamos supor que esse valor seja o nosso X, dessa forma nossa figura ficará
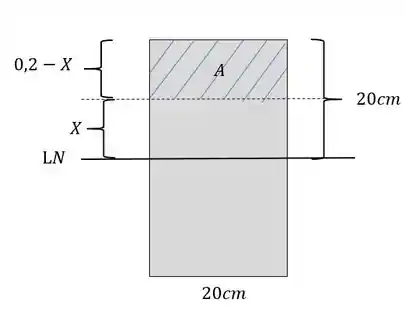
Então teremos que
Logo nosso momento estático será dado por
Passo 5
Agora que já determinamos todos os valores basta substituirmos na nossa equação
Substituindo teremos que
Ou seja, a nossa peça sofreria rompimento no trecho distante 18,6 cm da linha neutra, ou seja, antes mesmo do cisalhante máximo que ocorreria na Linha Neutra.
Resposta
Nossa peça sofre rompimento a altura de 18,6 cm com relação a Linha Neutra