Para a distribuição de velocidades a seguir, determine se existe uma função corrente e, se existir, encontre uma expressão para e faça o esboço da linha de corrente que passa pelo ponto .
Passo 1
A função corrente é definida em coordenadas cartesianas como:
Devemos aplicar o passo a passo
Passo 2
Seguindo o passo a passo, devemos escolher uma das duas equações do passo 1 para integrar. Vamos escolher a segunda:
Passo 3
Agora, derivamos a expressão obtida no passo anterior com relação a outra variável que aqui é , ou seja, calculamos
Calculando, temos
Passo 4
Usando a definição de função corrente, temos
Passo 5
Juntando tudo, temos que
Passo 6
Substituindo o ponto na equação acima, temos que
Assim, devemos plotar a seguinte curva
O que gera a imagem abaixo
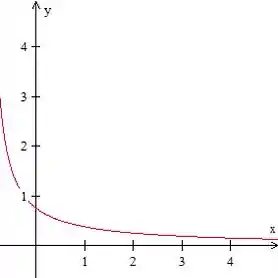
Resposta
Exercícios de Livros Relacionados
Considere que o barco a rotor Flettner da figura P8.54 tenha um coeficiente de resistência na água de 0,005. Com que rapidez o barco irá navegar na água do mar a 20°C sob um vento de 6,1 m/s se a quil
Uma corrente de água uniforme U ∞ =20m / s e ρ =998k g / m ³ ³ é combinada com uma fonte na origem para formar um semicorpo. Em (x, y) = (0, 1,2 m), a pressão é 12,5 kPa abaixo de p ∞ . (a) Esse ponto
Modifique o Problema 8.52 como se segue. Para os mesmos dados do veleiro, encontre a velocidade do vento, em km/h, que irá mover o barco a uma velocidade ótima de 4,1 m/s paralela à quilha.
Considere um escoamento com massa específica e viscosidade constantes. Se o escoamento possui um potencial de velocidades definido pela Equação ( 8.1 ) , mostre que ele satisfaz exatamente as equações
Uma central de energia descarrega água de refrigeração pelo distribuidor na Figura P 8.11 , que tem 55c m de diâmetro, 8m de altura e é perfurado com 25.000 orifícios de 1c m de diâmetro. O distribuid