Exame de Proeficiência de Pré-Cálculo da UFSC - 2019.2
Pré-Cálculo - UFSC
12. Em relação à equação , é possivel afirmar que
- Não admite solução real
- Admite apenas uma solução real
- Admite exatamente duas soluções reais
- Admite exatamente três soluções reais
- Admite exatamente quatro soluções reais.
5. Considere a função . Se é o intervalo que representa o domínio de , então é igual a
2. Considere as funções e . Se e são soluções da equação , então é igual a
É igual a
10. Seja um número real positivo e considere as funções
Assinale a alternativa verdadeira
- Nenhuma das alternativas
7. Assinale a alternativa verdadeira.
- Se é sobrejetora, então é sobrejetora.
- Se e são funções sobrejetoras, então é sobrejetora.
- Se e são funções injetoras, então é injetora.
- Se e são funções injetoras, então é injetora.
- Se é sobrejetora, então possui inversa.
18. Sejam e números reais tais que
Para todo . Sabendo que , então é igual a
Sugestão: Verifique o que acontece quando e quando .
Ver solução completa19. Sejam , e os vértices de um triângulo retângulo com ângulo reto em e sejam e as medidas dos catetos e , respectivamente. Se é o ponto médio do cateto , então a tangente do ângulo é igual a
20. Sejam e números reais positivos. Na figura abaixo, a linha pontilhada representa o gráfico da função e a linha contínua representa o gráfico da função .
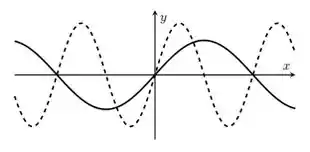
Pode-se afirmar que
- e
- e
- e
- e
- e
4. Sejam e números reais e considere o polinômio . Ao dividir por , o resto é e ao, dividir por , o resto é . Então o valor de é