Calcule
Onde é a região limitada pelas parábolas e .
Passo 1
Calma calma calma, antes de tudo vamos fazer um esboço para entender melhor o que está sendo pedido! Como as duas parábolas têm o coeficiente do termo positivos, elas estão viradas para cima. Fazendo , descobriremos suas raízes.
Então vamos lá, começando com a
Isso significa que nossa parábola toca o eixo quando .
Agora vamos olhar para , fazendo:
Opa! Isso aí não vai rolar porque não podemos tirar a raiz real de um número negativo. Isso significa que a segunda parábola não possui raízes reais, portanto, não corta o eixo , beleza? Ela está acima do eixo.
Pra desenharmos ela, vamos lembrar que ela é muito parecida com a parábola . A diferença é que ela tem o . Então, pra desenharmos ela, nós desenhamos a e subimos uma unidade no eixo . Certo?
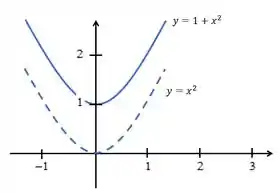
Agora que já descobrimos nossas duas parábolas, vamos colocar elas juntas em um gráfico. E vai ficar assim:
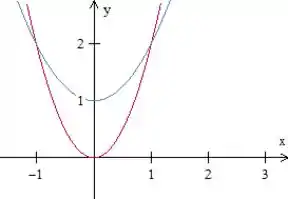
Passo 2
Perceba que as duas parábolas formaram uma região limitada por elas. Essa será a região de integração.
Como essa região está limitada em por duas funções (a parábola vermelha e a azul), em precisamos que ela esteja limitada por 2 números, para podermos escrevê-la como uma região do tipo I!
Já temos , sendo:
Para descobrir o intervalo em , devemos fazer e interseção entre as equações das parábolas e , ou seja, precisamos iguala-las. Assim descobriremos em que valores de a região começa e termina.
Fazendo
Jogando pro lado de cá da equação:
Tirando a raiz, teremos:
Assim, descobrimos que varia entre e (onde as curvas se encontram). Podemos, então, escrever a região como:
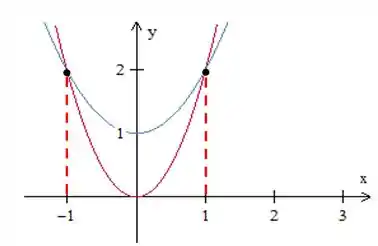
Passo 3
Vamos, então, substituir em nossa integral os valores que acabamos de encontrar para o domínio, beleza?
Mas cuidado com a ordem de integração! Lembre-se de que a variável que está variando entre funções fica na integral de dentro (no caso o , enquanto a variável que possui limites com números ficam na de fora (no caso o . Da seguinte forma:
Passo 4
Agora vamos integrar em relação a (integral de dentro):
Podemos simplificar o no segundo termos da solução da integral de dentro, ficando com:
Substituindo os limites de integração na variável , teremos:
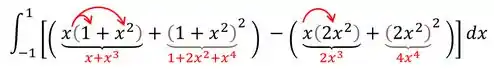
Aqui vamos ajeitar um pouco, fazendo as multiplicações:
O sinal de menos na frente do parênteses faz com que os sinais dos termos que estão lá dentro sejam alterados:
Finalmente reduzimos os temos semelhantes ficando com:
Passo 5
Está na hora, então, de integrar em relação a :
Substituindo os limites de integração ficaremos com:
Aqui vamos tirar os parênteses e consertar os sinais:
Veja que temos algumas parcelas que se cancelam:
![]()
Juntamos os números que tem o mesmo denominador:
E agora tiramos o m.m.c.
Prontinho, e depois de tudo isso chegamos a nossa resposta!