A integral fornece a área de uma região no plano . Esboce a região, identifique cada curva limite com sua equação, escreva as coordenadas dos pontos onde há intersecção das curvas. Depois encontre a área da região.
Passo 1
Vamos dar uma olhada nessa integral. O que ela nos diz?
Primeiro, ela diz que o está variando entre e e vemos isso pelos limites da integral de fora. Além disso, ela também nós diz que para cada um desses valores de , o varia de até , o que está representado nos limites da integral de dentro.
Vamos desenhar essas últimas duas funções!
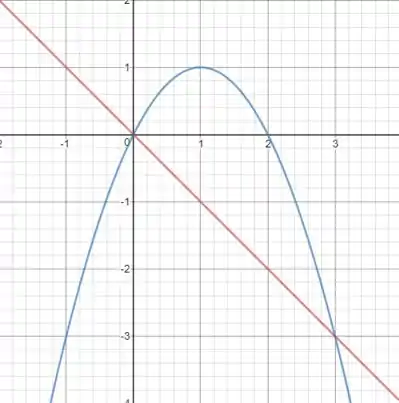
Beleza, para cada entre e o , vamos pegar toda a área entre a reta vermelha e a parábola azul! Então um esboço da área ficaria assim:
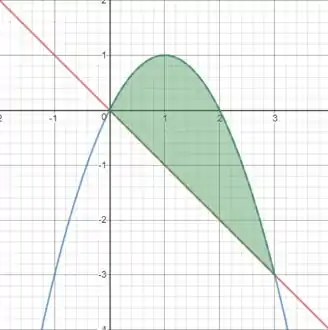
Beleza, fizemos a primeira parte.
Passo 2
Agora queremos saber quais são os pontos onde há interseção das curvas. Vamos fazer isso fingindo que não temos essas imagens aí de cima, usando só álgebra.
Ok, as duas funções são:
Vamos igualar as duas equações para achar os valores de em que as duas curvas se encontram!
Arrumando um pouco:
O que nós dá um equação de segundo grau pra resolver. Podemos fazer isso colocando o em evidência:
Então há duas possibilidades para essa multiplicação dar zero;
Ou
E isso dá pra gente
Beleza, essas são os valores de nos pontos em que e são iguais. Agora é só substituir esses valores em qualquer uma das duas funções pra achamos os valores de e assim determinarmos os pontos que o enunciado pediu:
Quando
Quando
Pronto, já temos as coordenadas dos dois pontos de interseção!
Passo 3
Finalmente, queremos a área da região, ou seja, queremos calcular aquela integral lá de cima!
Como a gente pode resolver essa integral dupla? Sempre começamos com a integral de dentro!
Substituindo os limites de integração, ficamos com:
Que nos dá
E agora é só integrar em relação a , que é a integral de fora. Vamos lembrar das seguintes “fórmulas”!
Então nossa integral fica
E agora é só substituir os limites de integração e calcular:
Isso dá
Ficando com:
Que nos dá
Prontinho, calculamos a área!
Resposta
Há intersecção das curvas nos pontos e . A área da região em questão é .