Considere a região plana definida por
Sejam uma função contínua definida em , e .
a) Esboce e, ao lado, esboce o interior de (ou seja, o conjunto aberto obtido removendo-se de a sua fronteira).
b) Escreva a integral dupla na forma de uma integral iterada, integrando primeiro com respeito a e depois com respeito a .
Passo 1
Oi, tudo bem? Vamos lá para mais um exercício!
a) Problema bem objetivo: pegue a definição de e a desenhe!
Como é função de , nesse primeiro momento, vamos trocar as desigualdades por igualdades.
Assim, temos que está entre as curvas e , certo? Então, só precisamos esboçar cada uma delas!
Se está entre e , vamos percorrer essa faixa de valores colocando na curva . Tá, e que curva é essa?
Bom, como o está no expoente, basta fazer algo que comece crescendo devagar, e dispare à medida que cresce ;)
E o gráfico vai ficar com essa carinha aqui:
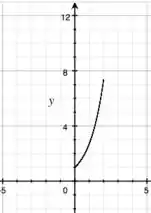
Passo 2
Show, agora temos que fazer para , beleza? Basta desenhar uma curva simétrica à do passo anterior em relação ao eixo , pois, para os mesmos valores de , teremos negativo:
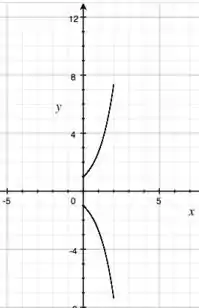
Lembrando que essas curvas param quando atinge valor !
Tranquilo até agora?
Passo 3
E, para fechar a curva, basta colocar dois segmentos de reta, um para fechar em e outro em !
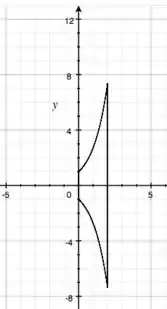
E esse é o contorno de ! Agora, temos que colocar as desigualdades de volta!
Pense no seguinte: Se estamos na curva de cima, temos que , então a região estará a baixo da curva (valores de menores que os valores da curva).
E, estando na curva de baixo, temos , então a região estará acima da curva (valores maiores que a curva).
Assim, é a curva que traçamos aí em cima, mais o interior dela! Essa dica ajuda muito na hora de ver regiões mais estranhas de integração ;)
Passo 4
Agora, o problema ainda pede pra tirarmos a fronteira de , ou seja, temos que esboçar apenas seu interior, certo? Então, só preencher, lembrando de excluir o contorno. E nossa região será representada por:
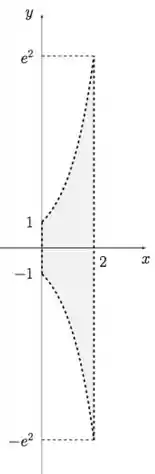
Passo 5
b) Agora é hora de escrever a integral, vamos lá!
Temos variando entre e , e variando entre as duas funções de , e . Assim, colocando primeiro em relação a e depois a (como deve ser, porque é função de !), temos:
Tranquilinho né? Hehe espero que sim!
Resposta
a) Contorno: 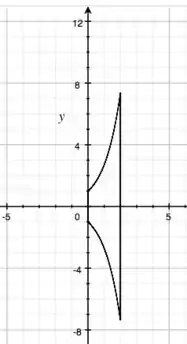
b)