Seja o domínio representado na figura, onde é a parte da circunferência , é a parte da circunferência , é a parte da circunferência . Reescrever a integral dupla
na forma iterada:
1. vendo como domínio de tipo 1
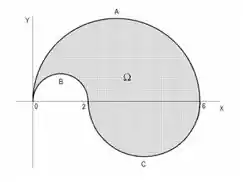
Passo 1
Falaa aí! Tudo certinho? Espero que sim porque vamos seguir com nosso estudo para ficar fera nessas integrais duplas do tipo 1!! 😊
Pra nossa sorte, a questão está pedindo pra gente simplesmente escrever a integral como uma integral do tipo 1, e não resolvê-la.
Então vamos lá. Precisamos lembrar que para escrever como uma integral do tipo 1, queremos o variando entre constantes, enquanto o varia entre funções, certo?
Bom, para isso então, vamos precisar separar em duas regiões:
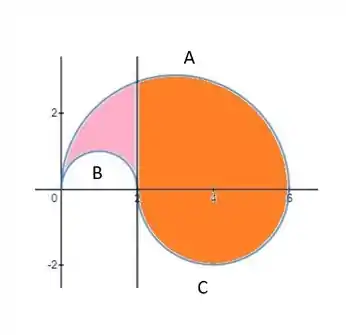
Temos à direita a região destacada laranja e a região à esquerda destacada de rosa. Precisamos fazer isso porque a função que está na parte de baixo da região muda exatamente no ponto com .
E quando fazemos isso, estamos matematicamente ajeitando nossa integral desse jeitinho aqui:
Passo 2
Vamos começar vendo nossa região rosa!
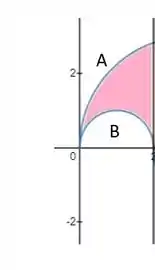
Se você for observar, podemos escrever que varia na região rosa de
Já para , temos que ela está variando desde a curva de baixo (que é a curva até a curva de cima (que é a curva .
Então nossa integral da curva rosa pode ser escrita assim:
Então vamos achar quem são essas funções e em relação a
Para temos essa equação dada no enunciado:
Isolando , temos
Tirando a raiz quadrada dos dois lados temos
(só vamos usar a parte positiva porque é a parte superior da nossa circunferência A)
Fazendo a mesma coisa para , temos que
Então, achamos nossos limites! Nossa integral fica assim:
Passo 3
Agora para região laranja temos isso aqui
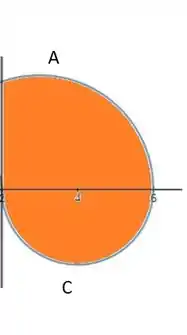
Se você for observar, podemos escrever que varia na região laranja de
Quanto à variação de , observamos que na região laranja vai de C até A.
Da mesma maneira que encontramos a função de , vamos fazer para :
Isolando
Tirando a raiz quadrada temos
(Maaaas se liga, como é a parte inferior da nossa circunferência C só vamos usar a parte negativa)
Então ficamos com:
Escrevendo a integral então ficamos:
Passo 4
Agora que já achamos as integrais das nossas duas áreas, vamos somá-las, lembrando que:
Então temos isso aqui:
Ufaaa! Prontinho, pessoal. Como o enunciado diz só para reescrever, não precisamos calcular (ainda bem né? Kk)