Determine o esboço da região do plano sobre a qual a integral é calculada:
Passo 1
Fala aí pessoal. Tudo certinho com vocês?
Bom o primeiro passo para resolver uma questão é sempre entender o que ela está pedindo, certo?
Aqui temos uma integral dupla, o que significa que ela será calculada sobre duas variáveis diferentes, a e a . Mas o que o enunciado quer é que a gente diga como é a região de integração. Então, o que temos que analisar são os limites de integração de e de que estão na integral dada.
Bora começar olhando o intervalo de integração que temos para , ou seja, o intervalo da integral de fora:
Com a separação das integrais, vemos que a que ficou na parte de fora dos colchetes está sendo calculado com o , então, assim podemos identificar os limites de integração em que são:
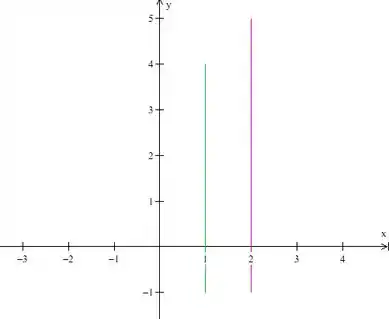
Como o enunciado pediu pra gente determinar no plano o esboço dessa região, já vamos delimitar lá no plano os valores de , que acabamos de identificar.
Agora já sabemos que no gráfico a região vai ficar entre essas duas retas fica assim:
Passo 2
Agora vamos olhar para os limites em , ou seja, a integral de dentro:
Veja que os limites indicam que nosso estão entre as curvas:
Isso quer dizer que temos as curvas e limitando nossa região. A primeira é uma parábola com concavidade para cima e que passa pela origem:
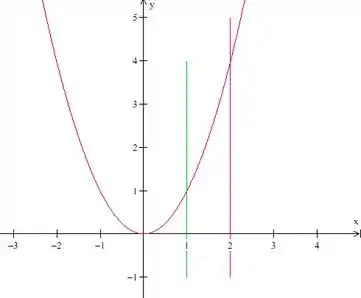
Agora vamos ver a outra curva, .
Passo 3
Como temos de um lado e do outro, sabemos que também é uma parábola, mas repare no sinal negativo de . Isso significa que a concavidade da parábola está voltada para baixo.
E mais: temos esse termo , que significa que ela está deslocada de alguma forma. Vamos calcular suas raízes para entender melhor como ficará esse gráfico, beleza?
Aqui podemos isolar o colocando ele em evidência:
Isso ajuda a gente a resolver mais rápido, pois temos uma multiplicação de por dando zero. Isso só pode acontecer se um deles for zero. Então, temos duas possibilidades
Ou,
Passo 4
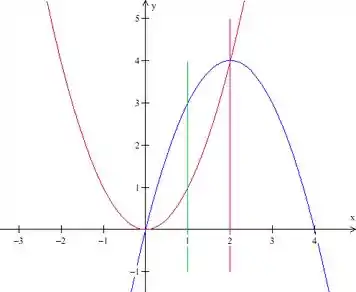
Com as nossas duas soluções:
Essas soluções dizem pra gente onde a nossa parábola vai cortar o eixo .
Temos que ela passa, então, pelos pontos e . Vamos desenhar isso aqui:
Passo 5
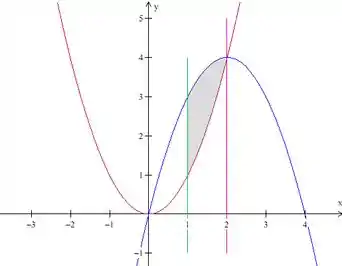
Show de bola, temos tudo desenhado, agora vamos identificar a região de integração, lembrando que:
E
Vamos pintar a região que fica limitada por essas curvas:
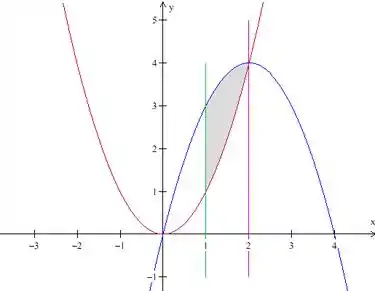
E essa é nossa região de integração. Show!!
Resposta
e
Com: