Exercícios de Integrais Duplas sobre Regiões do Tipo 1 - Lista de Exercícios Resolvida
Questão 2
Determine o esboço da região do plano sobre a qual a integral é calculada:
Ver solução completaQuestão 3
Suponha que uma lâmina com densidade ocupe a região do plano . Calcule a massa total sabendo que é a região triangular de vértices e a densidade em cada ponto é igual à distância de ao eixo
Ver solução completaQuestão 4
Sendo a região plana delimitada pelas curvas dadas pela equação e , calcule
Ver solução completaQuestão 5
Use integral dupla para calcular a área da região limitada por:
No primeiro quadrante.
Ver solução completaQuestão 7
Seja o domínio representado na figura, onde é a parte da circunferência , é a parte da circunferência , é a parte da circunferência . Reescrever a integral dupla
na forma iterada:
1. vendo como domínio de tipo 1
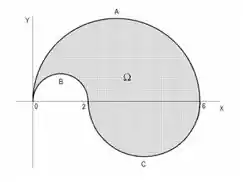
Questão 8
Considere a região plana definida por
Sejam uma função contínua definida em , e .
a) Esboce e, ao lado, esboce o interior de (ou seja, o conjunto aberto obtido removendo-se de a sua fronteira).
b) Escreva a integral dupla na forma de uma integral iterada, integrando primeiro com respeito a e depois com respeito a .
Ver solução completa