Sendo a região plana delimitada pelas curvas dadas pela equação e , calcule
Passo 1
Opa, vamos lá.
Pra facilitar a vida da gente, é legal a gente começar entendendo que região é essa que estamos trabalhando, pra isso nós desenhamos os gráficos de cada curva dada pelo enunciado.
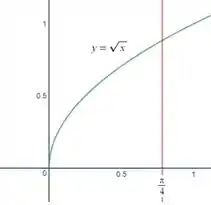
Em azul temos em vermelho temos e em verde!
Bom, só com isso a gente já tá com um bom caminho andando! Agora vamos descrever essa região que a gente tá vendo. Se você for observador, nosso varia de zero até ,
e nosso varia de zero até a função que está em cima, que é .
Show, então vamos escrever isso na integral.
Passo 2
Nosso passo 2 agora vai ser escrever o que a gente observou. Como vamos ficar?
Lembrando de colocar a variável que está limitada por funções pra ser a integral de dentro (no caso o ), e a variável que está variando entre números pra ser a integral de fora (no caso o ).
Passo 3
Por último, mas não menos importante, vamos resolver essa parada, depois é só correr pra o abraço. A nossa integral é
Começando pela integral de dentro, temos que
Vamos ter que fazer uma substituição simples, fazendo isso aqui
Derivando em relação a , temos
Então ficamos com
Podemos simplificar a , ficando com
Agora fica mais fácil de integral. Integrando isso daí, temos:
Voltando para , ficamos com:
Substituindo os limites de integração, temos:
O que nos dá:
E isso fica
Passo 4
Agora pegando isso e colocando na integral de fora, ficamos com:
Integrando:
Aplicamos os limites de integração:
Isso fica
Isso dá pra gente:
E assim conseguimos resolver a integral sob a região dada.