Encontrar as coordenadas do vértice, o foco e a equação da diretriz de cada uma das seguintes parábolas:

a)

Essa expressão tem o jeito parecido de uma das equações que vimos na teoria, que é a seguinte:

Vimos também que essa equação é a equação de uma parábola que possui vértice na origem e seu eixo é o eixo . Bom, já temos o vértice e o eixo só de lembrar da teoria. Também sabemos, que com essas características o foco é . Mas, quem é ?

Para achar devemos comparar

Comparando, temos:

Então,

E nossa, diretriz?

A diretriz está sempre a uma distância do vértice, como nosso foco está na parte positiva,então isso indica que nossa diretriz estará na parte negativa:

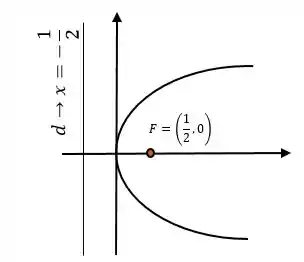
Portanto, nossa diretriz é:

Pronto!! Nossa primeira parábola já está definida:

b)

Essa equação não se parece nem com o caso 1 e nem com o caso 2, mas com o caso 3, que possui translação!! É isso mesmo!!

Como vimos, para resolver esse tipo de exercício primeiro passamos a equação para um sistema genérico , resolvemos tudo para esse sistema e depois passamos para o sistema cartesiano novamente.

Então, nosso sistema genérico será:

Fazendo essas mudanças, teremos:

Vamos resolver, normalmente! Então primeiro, vamos encontrar o valor de :

Comparando:

Nosso foco no sistema será:

O vértice no sistema é .

Como temos que nosso foco está na parte negativa, então nossa reta diretriz estará na parte positiva e será . Logo,

Sempre lembre que o foco e a diretriz são simétricos em relação a algum dos eixos.

Bom, chegamos em todos os resultados, mas os resultados está no sistema , então chegou a hora de usarmos as relações,

Para passarmos do para .

Assim, para o sistema temos:

Substituindo as relações e ,temos:

Nossa parábola nos eixos possuem os seguintes elementos:

c)

Esse item é parecido com o anterior, o que vai alterar são as relações de e .

Então, primeiro escrevendo essas relações, temos:

Assim, teremos a expressão em :

Vamos tratar esse problema normalmente só que a diferença é que estamos num sistema de coordenadas , mas isso resolvemos depois ;).

Pelo jeito da expressão sabemos que o eixo da nossa parábola é o eixo e que o vértice no sistema é . Vamos encontrar o valor de para acharmos o foco e a diretriz!!

Comparando, temos:

Nosso foco no sistema é ,portanto:

Como nosso foco está no lado positivo, nossa diretriz estará no negativo, então:

Pronto! O problema terminou!! Nada disso!! Cuidado, achamos os resultados para o sistema genérico , mas as respostas sempre devemos dar em coordenadas cartesianas . Então, para terminar vamos usar as relações:

Substituindo, temos:

Agora, sim!! Nossas respostas são:,

d)

Nesse item não temos mais translação, mas note que agora quem está elevado ao quadrado éo e não mais o como estávamos fazendo. Então, agora, estamos no 1º caso da teoria.

Se estamos no 1º caso da teoria sabemos que o vértice é e que o eixo da parábola será, agora, o eixo dos . Falta, então, calcularmos o valor de para então descobrirmos as coordenadas do foco e a reta diretriz.

Então, comparando:

Nosso foco nesse caso é como vimos na teoria. Achamos que , substituindo temos:

Como nosso foco é negativo, a diretriz estará na parte positiva como mostra a figura:

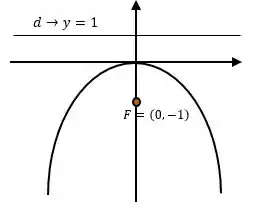
Calculando será:

Pronto!! Como não tivemos que fazernenhuma mudança de coordenadas todos os nossos resultados já estão nas coordenadas . Então, temos como resultado: e .

e)

Nosso problema agora é parecido com o do item anterior, mas com translação, ou seja, teremos que fazer uma mudança de coordenadas. Para isso, vamos excrever as relações:

Substituindo essas relações obtemos a seguinte expressão no sistema :

Agora, estamos no caso do item anterior, mas num sistema transladado. Vamos calcularos parâmetros normalmente e depois fazemos a mudança de coordenadas. Pelo jeitão da expressão estamos no primeiro caso, ou seja, e nosso eixo é o eixo . Lembrando, como fizemos uma mudança de variável trabalharemos com o sistema . Podemos comparar então:

Da teoria sabemos, que , então nosso foco no sistema fica:

E nossa diretriz, também no sistema é . Como nosso foco está na parte negativa, nossoa diretriz estará na parte positiva, então:

Já que achamos tudo o que precisávamos no sistema , agora sim, podemos passar para o sistema . Para isso vamos utilizar as relações:

Substituindo, teremos:

Terminamos!! A solução desse item é: , e .