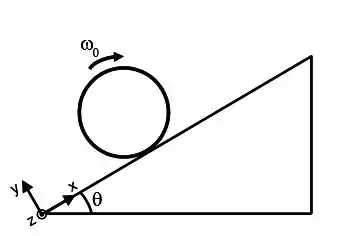
Após sofrer um impulso, um aro de massa e raio rola sem deslizar plano acima. O plano está inclinado de em relação à horizontal. No instante de tempo o aro tem velocidade angular de módulo e está na posição a partir da origem. Suponha que o plano é suficientemente longo e que o aro alcança sua altura máxima a uma distância . Após parar momentaneamente o aro rola sem deslizar plano abaixo. Utilize para a aceleração da gravidade e o sistema de eixos indicado.
(a) Determine o momento de inércia rotacional do aro em relação ao ponto de contato com o plano inclinado.
(b) Determine a distância em função dos dados do problema.
(c) Determine o torque da força de atrito em torno do centro do aro, quando ele estiver momentaneamente parado, prestes a rolar sem deslizar plano abaixo.
Passo 1
(a) Pelo teorema dos eixos paralelos temos:
Passo 2
(b) A energia mecânica se conserva, então:
Portanto, devemos contar com a variação da energia potencial gravitacional como:
E a variação da energia cinética:
Onde:
E:
Logo:
Passo 3
(c)
Pela segunda lei de Newton, temos, pela análise das forças:
Já para a segunda lei de Newton da rotação:
Como:
Temos:
Somando e temos:
Substituindo na equação (1):
E então:
Resposta
a)
b)
c)