Seja uma função contínua no intervalo fechado , onde e .
Qual das sentenças abaixo é verdadeira, observando o teorema de valor intermediário?
- para pelo menos um entre e
- para pelo menos um entre e
- para pelo menos um entre e 7
- para pelo menos um entre e
Passo 1
Vamos láá!! Antes de mais nada, vamos relembrar o que nos diz o teorema do valor intermediário???

O teorema do valor intermediário diz que se temos um função contínua em um intervalo fechado e além disso temos um número qualquer entre e , em que então existe um número em tal que
Ficou confuso?
Sim?
Vamos colocar as informações do nosso enunciado num gráfico para visualizar melhor?!
Passo 2
Pegando as informações do enunciado e colocando num plano cartesiano, temos
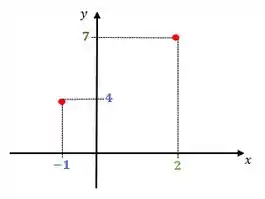
Beleza?!
Agora olhando pra descrição do teorema do valor intermediário, temos um número entre e , de tal forma que vai existir um outro número entre e tal que .

Tá... Quem são os nossos e nesse exercício? São e , concorda? E, de acordo com o enunciado,
E
Ou seja, temos um número que está entre e :
A segunda parte do teorema vai nos garantir que existe um número em tal que , e esse já sabemos que está entre e !!! Ou seja, já podemos descartar as letras B e D!
Beleza?!
Então já “traduzimos” pro nosso probleminha a primeira parte do teorema! Vamos agora pra segunda parte!
Passo 3
Já sabemos que o nosso número está entre e , agora o teorema diz que existe um em tal que Quem vão ser as letras e nesse exercício?

Se você reparar, e são os extremos do intervalo que são substituídos dentro da função! Ou seja,
E
Portanto, para pelo menos um entre e !! Visualizando graficamente, teremos
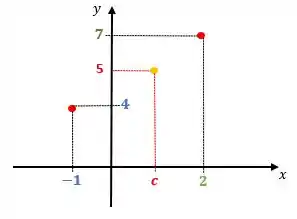
Show de bola?!
Assim, a nossa resposta é a letra C!
Resposta
Letra C