Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Transformação de Lorentz para Espaço e Tempo

Ver Teoria
Exercício 123456789101112131415

Enunciado

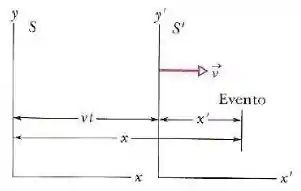
Como na figura abaixo, o referencial S ' passa pelo referencial S com uma certa velocidade.

A figura abaixo mostra a distância temporal entre dois eventos no referencial S , Δ t , em função da distância espacial entre os mesmos eventos no referencial S ' , Δ x ' , para 0 ≤ Δ x ' ≤ 400 m . A escala do eixo vertical é definida por Δ t a = 6,00   μ s .

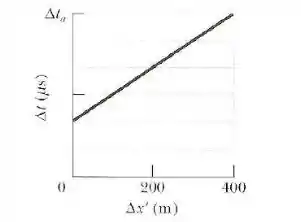
Qual é o valor da distância temporal entre os dois eventos no referencial S ' , Δ t ' ?

Passo 1

Usando a transformação de Lorentz para o tempo, temos:

Δ t = γ Δ t ' + u Δ x ' c 2

Aqui é necessária uma certa malandragem... nós podemos usar pegar essa equação, ajeitá-la pra compararmos com o gráfico e tirar algumas conclusões, se liga:

Δ t = γ Δ t ' + Δ x ' u γ c 2

Se compararmos essa equação com o gráfico, podemos ver que Δ t e Δ x ' são linearmente dependentes. Ou seja, a relação entre os dois tem essa cara:

Δ t = a Δ x ' + b

Onde a e b são os coeficientes angular e linear, respectivamente.

Vamos usar as informações do gráfico pra calcular os coeficientes.

Passo 2

  • Coeficiente angular a :

O coeficiente angular é dado pela inclinação da reta, logo, usando a escala do gráfico:

a = 6 - 2 400 - 0 = 10 - 2 μ s / m

a = 10 - 8   s / m

Onde, de acordo com a equação:

a = u γ c 2

Beleza, daqui vamos conseguir (com um certo trabalho) calcular a velocidade u . Então, partiu! #fénopai #queoinimigocai

10 - 8 = u γ 3 × 10 8 2

u γ = 9 × 10 8

Substituindo a expressão de γ , teremos:

u 1 - u 2 c 2 = 9 × 10 8

1 1 u 1 - u 2 c 2 = 9 × 10 8

1 1 u 2 - 1 c 2 = 9 × 10 8

Elevando os dois lados ao quadrado:

1 1 u 2 - 1 c 2 = 8,1 × 10 17

1 u 2 - 1 c 2 = 1,23 × 10 - 18

1 u 2 = 1,23 × 10 - 18 + 1 3 × 10 8 2

1 u 2 = 1,23 × 10 - 17

Finalmente:

u = 2,85 × 10 8   m / s

Eu sei... foi chato demais.

Passo 3

Agora podemos determinar o fator de Lorentz, através da equação:

γ = 1 1 - u c 2

Substituindo os valores das velocidades:

γ = 1 1 - 2,85 × 10 8 3 × 10 8 2

γ = 3 , 2

Passo 4

Voltando para a transformação de Lorentz:

Δ t = γ Δ t ' + Δ x ' u γ c 2

Pra simplificar os cálculos, vamos escolher no gráfico o ponto em eu Δ x ' = 0 e Δ t = 2,0   μ s . Logo:

Δ t = γ Δ t ' → Δ t ' = Δ t γ

Substituindo os valores, teremos:

Δ t ' = 2 × 10 - 6 3,2

Δ t ' = 6,25 × 10 - 7 s

Resposta

Δ t ' = 6,2 5 × 10 - 7 s

Exercícios de Livros Relacionados

65 . Suponha que nosso Sol esteja para explodir. Em um esforço para fugir, partimos em uma espaçonave com v=0,800 c em direção à estrela Tau Ceti, a 12,0 anos-luz de distância. Quando alcançamos a met
61. Um sistrema S ' possui um componente x da velocidade igual a u relativa um sistema S e para t = t ' = 0 os dois sistemas coincidem (Figura 37.3 ). Um pulso de luz é emitido na origem de S ' no ins
No quadro S, o evento B ocorre 2,0 μs após o evento A, e o evento A ocorre na origem, enquanto o evento B ocorre no eixo x em x = 1,5 km. Com que velocidade e em que direção um observador deve estar v
A equação para a frente de onda esférica de um pulso de luz que começa na origem no tempo t = 0 é x2 + y2 + z2 - (ct) 2 = 0. O quadro S ′ se move com velocidade v ao longo do eixo x. Usando a transfor
Uma longa haste paralela ao eixo x é liberada do repouso. Subsequentemente, ele está em queda livre com uma aceleração de magnitude g na direção –y. Um observador em um foguete se movendo com velocida