Exercícios de Energia Total Relativística - Lista de Exercícios Resolvida

Um próton e um elétron são acelerados até que suas energias totais sejam o dobro das suas respectivas energias de repouso.

Sendo a energia de repouso do próton e a do elétron , a razão entre as velocidades do próton e do elétron é:

6. Nenhuma das anteriores

Qual é a velocidade de uma partícula cuja energia cinética é

1. Igual à energia de repouso?
2. Cinco vezes maior do que o valor de sua energia de repouso?

um nêutron de tem energia cinética maior, menor ou igual à energia total de um elétron de ? Justifique.

Obs:

Quando dizemos que se trata de “um elétron de ”, isso quer dizer que sua energia cinética é .

um nêutron de tem nergia cinética maior, menor ou igual à energia total de um elétron de ? Justifique.

Uma partícula instável, de massa de repouso , inicialmente em repouso, decai produzindo duas partículas idênticas. Suponha que a massa de repouso e a energia cinética K de cada uma das partículas finais sejam conhecidas. Considere também que o sistema permanece isolado ao longo de todo o processo.

(a) Seja v a velocidade de uma das partículas de massa de repouso . Calcule v/c, onde c é a velocidade da luz no vácuo. Expresse sua resposta em termos de, K e c.

(b) Calcule o valor da massa , expressando sua resposta em termos de , K e c.

(c) Determine v, quando = 0.

Um acelerador de partícula é projetado de tal forma que a maior energia total alcançada pela partícula vale dez vezes (10) a energia de repouso da partícula. Nesse acelerador, a velocidade máxima alcançada pela partícula é dada por?

a)

b)

c)

d)

e)

f)

A variável na equação de Einstein significa:

1-( ) a energia total de um objeto de massa m.

2-( ) a energia equivalente à massa que uma partícula possui quando está em repouso.

3-( ) a energia cinética relativística de uma partícula de massa m.

4-( ) a energia máxima que um objeto de massa m pode possuir.

Na relatividade restrita, qual das seguintes propriedades de um corpo é independente da velocidade desse corpo?

a) Massa de repouso.

b) Massa relativística.

c) Energia cinética.

d) Energia total.

e) Momento linear.

Quando a velocidade de uma partícula de massa de repouso se aproxima da velocidade da luz, sua massa relativística se aproxima de

a) Zero.

b) .

c) .

d) Infinito.

e) Não é possível determinar.

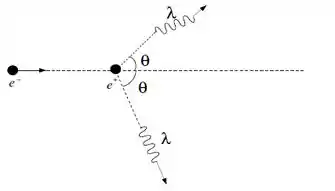
Um elétron, com massa de repouso e energia cinética colide com um pósitron em repouso produzindo dois fótons, conforme ilustrado na figura abaixo. O pósitron é uma partícula com a mesma massa de repouso do elétron, porém com carga oposta.

Determine o comprimento de onda dos fótons em função de e .

Encontre o ângulo de espalhamento.

Faça a escolha correta e justifique:

A - Na Mecânica Quântica, quando um átomo absorve um fóton:

(a ) a massa do átomo aumenta.

(b ) a energia do átomo aumenta.

(c ) a massa do átomo diminui.

(d ) o átomo não sofre uma transição quântica.

Um próton e um elétron são acelerados até que suas energias totais sejam o dobro das suas respectivas energias de repouso.

Sendo a energia de repouso do próton e a do elétron , a razão entre as velocidades do próton e do elétron é:

6. Nenhuma das anteriores